采用FPGA实现多项式运算

传统的DSP都基于CPU结构，是一种基于特定指令系统的处理器，但随着运算时钟越来越接近电子器件可以接受的极限，这种DSP的处理能力也在接近它的极限；另一方面随着EDA技术的发展，尤其像FPGA和CPLD器件的成熟和应用，可以通过直接设计电路来实现并行的运算，这样运算的效率从本质上得到了提高，而且目前能实时地实现非常复杂的运算，所以基于FPGA的运算器被提上议事日程，并受到越来越多的重视。一种便于用电路实现而且通用性强的算法，可以帮助工程师简单高效地完成一个能在FPGA上工作的运算器的设计。

1 数字电路实现运算的优缺点

初步的FPGA设计是用硬件描述语言完成器件逻辑功能的描述，一个好的设计必须考虑数字电路的特点。CPU是一个典型的数字电路，因为其只能做加法运算，所以需要通过程序将各种运算都转换为加法来完成。传统的“数值分析”正是在这种程序设计的基础上形成的，不但复杂而且效率不高，不能实现真正的实时运算，而FPGA本身除了能做加法运算外，做无符号数的减法和乘法也很方便。目前两大FPGA生产商推出的集成开发软件中，都有集成的加、减法和乘法的IP核，运算效率非常高，对于无符号数的运算一般只要1个时钟，甚至是不需要时钟的组合逻辑电路，文献中也有这些运算器的详细介绍。但是直接做除法则不同，虽然也有除法IP核，但是需要许多个时钟，而且占用逻辑资源很多，无论设计还是应用都不方便。电路运算的另一个缺点是表示有符号数和小数，以及做有符号小数间的运算也很麻烦。所以在设计DSP时总是希望能够找到一种方法尽量的趋易避难。

2 麦克劳林级数和多项式

运算器的作用是对数据进行各种运算，这个过程可以用一个函数来表示：y=f(x)。任何一个在零附近连续的函数都可以展开为麦克劳林级数：

大部分常用函数的高阶导数项很小或者为零，所以在精度允许的范围内取其中的有限项就可以，即用一个多项式做近似运算，多项式运算的特点在文献中有详细介绍。用FPGA实现多项式的运算，处理很多复杂的函数将会十分方便。
y=a0+a1×x+a2×x2+…+an×xn (2)

本文讨论的是一种可以用FPGA或CPLD实现多项式(2)运算的运算器。对于简单的多项式可以是一个组合逻辑电路，不需要时钟，所以运算效率很高。这样许多运算都可以简单而且高效的完成。

3 运算器设计 3．1 四则运算电路

文献中瞄述了各种无符号整数间的运算电路。虽然也可以进行用反码表示的符号数的运算，但不倾向于使用。因为需要做四则混合运算；反码易于做加、减法，但不易做乘、除法。而用非反码的带符号位的数据，符号位做单独计算，其余数据做无符号运算，整个计算结构是最简单的。另外即便是无符号数做除法也很复杂，不过考虑到有种特殊的除法运算除外，那就是对于二进制数去掉最末位就相当于除以2。所以运算时可以尽量避免除以非2倍数的数，以此来简化计算。
表示小数在计算中是必须的。文献中介绍了二进制定点小数，比如需要保留数的2位二进制小数位，可以将二进制小数“…b3b2b1．a1 a2”表示为：

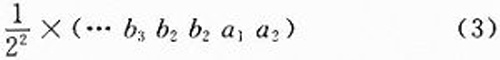
运算中还是可以视为对整数的计算。这样用无符号的定点数进行计算，配合独立的符号位表示正负，就可以用简单的无符号运算器进行复杂的运算。

3．2 多项式的变换

式(4)为一个3次多项式，以它为例来介绍设计方法：
y=a0+a1×x+a2×x2+a3×x3 (4)

首先将式(4)中所有的数都用一个符号位加无符号二进制形式表示。分别用N1，N2表示y和x中包含的小数位数，可以将式(4)写成：

式中：X，Y是x，y去掉小数点后的整数(注：这里和式(3)一样只是去掉小数点，不是去掉小数位)。A0，A1，A2，A3作为系统的常数也是一样；n0，n1，n2，n3分别是a0，a1，a2，a3二进制形式的小数位数。可以进一步变换式(5)为：

 

不难发现式(6)是很容易实现的。先进行各项符号位的计算，然后就只剩下无符号整形数据计算；而且除法全是除以2的倍数。最后各项之间根据符号位做加、减运算就得到输出Y，是带符号有N1位小数的定点数。