
1、引言
带A/D转换器(ADC)和脉冲宽度调制器(PWM)等集成外设的低成本高性能数字信号处理器(DSP),已在电机控制、不间断电源(UPS)和运动控制等领域获得比较广泛的应用。低成本DSP在控制电源变换功能方面,为电源设计者提供了新的工具。
与传统模拟控制比较,DSP控制器具有许多突出的优点,例如多平台标准硬件设计、对老化和环境变化的低敏感度、优异的抗噪扰性、易于履行高级控制算法、设计变更的灵活性及控制和通信功能的单芯片解决等。然而,在电源设计中使用DSP,对许多模拟设计者来说面临新的挑战,他们必须尽力改变设计,以适应新的数字环境。
本文以由德州仪器TMS320LF2407A 16位定点DSP控制的平均电流型功率因数校正(PFC)升压变换器为例,来说明与传统模拟设计方案存在的不同。在模拟控制领域不同的控制环路参数,必须重新定义到它们的数字履行上,然后进行环路分析,并给出要求的电压和电流环路补偿器,最后介绍这些补偿器的分立化及它们在软件中的执行。通过PFC级数字控制器设计为例,可以识别模拟与数字控制之间的基本区别。
2、TMS320LF2407A控制的PFC级电路
图1所示为由TMS320LF2407A控制的PFC级电路。该拓扑是一种AC-DC升压变换器,为履行控制算法(algorithm),需要三个信号,即整流的输入电压Vin、电感器电流Iin和DC总线(输出电容Co)电压V。
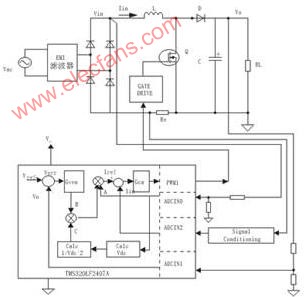
图1 TMS320LF2407A控制的PFC级电路
变换器由两个反馈环路控制:平均输出电压由较慢响应的外环调节,而整形输入电流的内环响应速度比外环快得多。瞬时信号Vin、Iin和Vo通过各自的电压和电流感测电路被检测,检测信号经三个数模转换器(ADC)信道反馈到DSP。这三个ADC通道分别是ADC/NO、ADCIN1和ADCIN2。这些信号的速率利用ADC控制环路的采样频率fs感测和转换。数字化感测的总线(bus)电压Vo与期望的参考总线电压Vref相比较,尔后将差分信号(Vref-Vo)馈入到电压环路控制器Gvea。数字化控制器Gvea的输出“B”与其它两个信号“A”和“C”相乘,为内部电流环路产生参考电流命令。在图1中,“A”代表感测的数字瞬时信号Vin。“C”可由下式确定: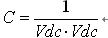
式中,Vdc是计算的感测数字化信号Vin的平均成分。在图1中的Iref是内部电流环路的参考电流命令,Iref具有经整流的正弦波形状,其幅度对于负载和AC线路电压的变化足以保持输出电压在一个参考电平Vref上。感测的数字化电感电流Iin与参考电流Iref进行比较,Iref与Iin之差值进入电流控制器Gca。Gca的输出最后为PFC开关产生PWM占空比命令。
3、PFC级数字控制器设计
图1所示的DSP控制的PFC变换器控制环路框图如图2所示。图中,Kf、Ks和Kd增益块替代了先前各自的电压和电流感测与调节电路。乘法器增益Km也加进控制单元中。Km允许参考信号Iref根据变换器输入工作电压范围进行调节。内部电流环路利用Iref来编程,电流环路功率级输入占空比命令是电感电流Iin。电流控制器Gca产生适当的控制输出Uca,致使Iin跟随Iref。电压控制器Gvea输出Unv输入到电压环路功率级,其输出是总线电压Vo。Gvea产生适当的Unv控制Iref的幅值,使Vo保持在参考电平上。德州仪器(TI)公司生产的TMS320LF2407A是一种16位定点(fixed-point)DSP控制器,被用作控制通用输入(85~265Vac)平均电流模式PFC预变换器。
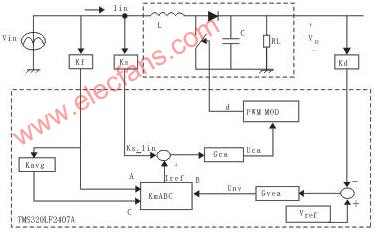
图2 TMS320LF2407A控制的PFC级控制环路框图
3.1 电压与电流感测增益
输入电压Vin和输入电流Iin分别表示为
Vin=Vm Sin2wt 0≤Vm≤Vmax
Iin=Im sin2wt 0≤Im≤Imax
式中:Vmax为峰值幅度Vm最大值,V;Imax为峰值幅度Im的最大值,A。
基于DSP的PFC变换器信号通过芯片上的A/D转换器感测。为使这些信号进入A/D转换器的范围之内,利用适当的外部调节电路加至每个通道。用户软件读出变换的信号,即数字化信号。从ADC结果寄存器读出的数字化信号,用适当的定点格式保存在临时存储器单元。数字化信号用有限的字长被表示为数值。在16位DSP中,最低位(LSB)用作表示信号的尾数,最高位(MSB)用作代表其符号。为了实现转换,需要选择信号的范围,然后在定点表示的整个范围之内标记变化结果的全部范围。对于TMS320LF2407A DSP,正向信号的范围是从0到32767。一旦这个映像完成,下一步则是为这些数字化信号选择适当的定点算法计数法。对于16位DSP,利用Q15计数法作为这些信号的定点表示是有利的。用这种表示方法,数值在0~32767范围之内,表示绝对值在0与1之间。用Q15计数法,电压和电流相对于它们的最大值作为规格化的每单位(pu)数值被自动保存。
在图2中,前馈电压感测增益Kf、电流感测增益Ks和PFC输出直流总线电压感测增益Kd分别表示为:
Kf=1/Vmax
Ks=1/Imax
Kd=1/Vo(max)
式中,Vmax为整流的输入电压Vin最大允许幅值,V;Imax为输入电流Iin的最大允许幅值,A;Vo(max)为直流总线电压最大允许值,V。
3.2 输入电压前馈软件的实现
输入电压前馈能使输入功率保持在规定的电平上,不随AC线路电压波动而变化。
为计算输入电压Vin的平均成分Vdc,需要计算信号频率f(=1/t),然后对一个周期上的信号进行积分,如图3示图所描述。
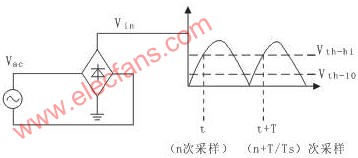
图3 和Vin平均成分的计算
3.2.1 频率计算
在频率软件执行期间和其后的平均Vin的计算,每当信号跨越上门限Uth-hi时,Vin的采样数(N)被计数并被保存。信号的下门限Uth-Io用于获得抗扰度。若采样周期为Ts,采样频率为fs=1/Ts。Vin的周期为T,N=T/Ts。若N为已知数,每单位(per unit, Pu)频率fpu的计算公式是: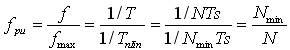
式中,fmax为Uin的最大频率,Hz;Nmin为Uin一个周期上的采样最小数。计算频率的用户软件利用N值,首先计算中间值1/N,然后与Nmin相乘得到fpu值。为保存1/N值,并带最高精度,不引起累加器溢出,知道Nmin值是很重要的。为此,用户应当选择信号最大频率以被测量。一旦知道Nmin值,1/N量可以被保存,并带最大精度且用适当的定点表示。例如,对于一个输入工作频率为47~63Hz的PFC变换器,最大输入频率可以选择70Hz。然后用fmax=140Hz(两倍的输入频率)和已知的Ts值来计算Nmin,是非常容易的。
3.2.2 前馈成分计算
只要知道信号Vin的频率,它的平均成分Vdc可用下面公式计算: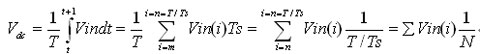
式中,T为相应于Uin频率f的时间周期, S;Vin(i)为Vin的数字化i次采样。
由于Vin作为相对于它的最大值Vmax的每单位(pu)规格化值被测量,所计算的Vdc值也是一个带Vmax规格化基本值的每单位(pu)量值。对于一个正弦波输入电压,Vac的最大值仅为2Vmax/π。因此,在Vac的固定点表示中,为获得最佳精度,先前计算的值相对于它自己的最大值被转换为每单位规格化量值,这个值由下式给出: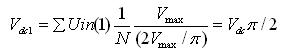
Vdc1的倒置电压Vinv(即Vinv=1/Vdc1)在Vdc1最小时值最大,反之亦然。为在Vinv固定点表示中获得较高的精度,需要用相对于其最大值的每单位(pu)规格化值来表示。对于一个正弦波输入电压,Vdc的最小值是2Vmin/π。输入电压最小幅值Vmin的选择,基于PFC变换器的输入电压范围。例如:若PFC变换器的低线路RMS电压是90V,Vmin值应低于或等于127V( )。Vinv的最大值为(Vminπ/2),相对于它自己最大值的相应Vinv的每单位(pu)值为: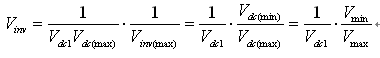
3.3 乘法器增益Km
乘法器增益Km的调节,应能在最低输入电压上,当PFC变换器交付最大负载时,使参考电流Iref是在它的最大值上。在图2中,Iref为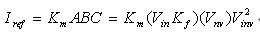
随电流环路闭合,Iref可表示为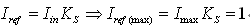
在最低工作电压Vinv=1时,满载下的电压控制器输出将在它的最大值上,即Vnv=1。因此,在最低工作电压上,为产生最大参考电流,要求Km值为: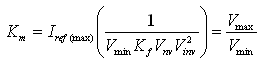
3.4 电压和电流环路补偿器
电流环路功率级高频近似值为: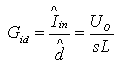
根据图2所示的PFC控制框图,电流环路增益等式为: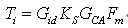
式中,Fm为调制器增益, 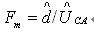
调制器在软件中部分地执行,并部分地利用DSP PWM硬件。软件利用调制器输入,即电流控制器输出Uca,计算在TMS320LF2407A中PWM硬件模块的占空比值。PWM硬件利用占空比值,为PFC开关产生适当的PWM信号。当调制器输入Uca是1时,软件保证调制器输出即PWM占空比为100%。在此情况下,调制器增益Fm=1。因此,对于电流环路的交越频率fci,需要的电流误差放大器补偿器可以表示为: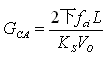
只要电流环路闭合,电压环路功率级传输函数可按下式计算: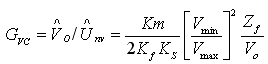
式中,Zf为输出电容CO和负载阻抗ZO组成的并联分支的等效阻抗,Zf=ZO/(1+sCOZO);负载阻抗 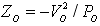 。
。
图2中电压环路增益等式如下: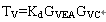
电压环路交越频率fcv需要的电压误差放大器补偿器为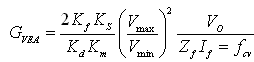
3.5 电压和电流环路补偿器软件的实现
先前给出的电压和电流环路控制器,在它们利用TMS320LF2407A在软件中被执行之前,被变换为如下说明的等效数字形式,电流控制器可以写为: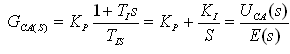
式中:KP为已计算的电流补偿器量值;E为电流误差信号。
电流环路补偿波德(Bode)曲线如图4所示。其中:顶部为电流环路控制单元增益Gid、Fm和KS曲线;中间为补偿器Gca增益曲线;底部为所期望的环路增益TI曲线。功率级有一个-1的斜率,在期望的穿越频率fci上放置零点fz,可以产生一个45°的相补角。然而,由于控制环路采样和补偿延时,相补角的一部分被损失,因此将fz放置到图4所指示的位置,以补偿相补角损失。
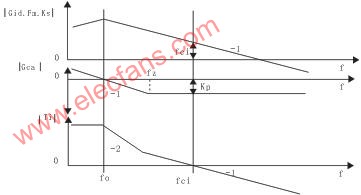
图4 电流环路补偿波德曲线
4、PFC级数字控制器设计实例
在本设计中的系统参数如下:
输出功率PO=825W,DC总线电压VO=380V,开关频率fSW=120KHz,数字环路采用频率fS=60KHz,L=100μH,C=390μF,fCV=10Hz,fci=8KHz,输入电压最大频率fmax=200Hz,Vmax=410V,Vmin=109.95V,Vo(max)=410V,输入电流最大值Imax=2PO/Vmin=15A。
各种增益参数分别为:kf=1/410,kd=1/410,KS=1/15,Km=410/109.95=3.7286。
4.1 电流控制器履行例子
由于fci=8KHz,电流控制器量值为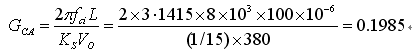
将电流环路PI补偿器零点设置在800Hz,电流补偿器的积分时间常数为TIC=1/2π×800=198.94×10-6。因此,完整的电流环路控制器为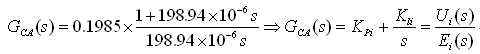
式中:KPi=0.1985,Kli=997.77。
分立(discrete)控制器执行等式为
Ui(n)=K0i?Ei(n)+li(n-1);
li(n)=li(n-1)+K1i?Ei(n)+Kcorri?Epii
Epii=Usi-Ui(n)
式中:当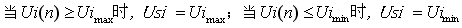 在其它情况下,
在其它情况下,
电流控制器相关系数为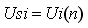 。
。
电流控制器相关系数为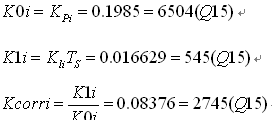
控制器履行的代码段如下:
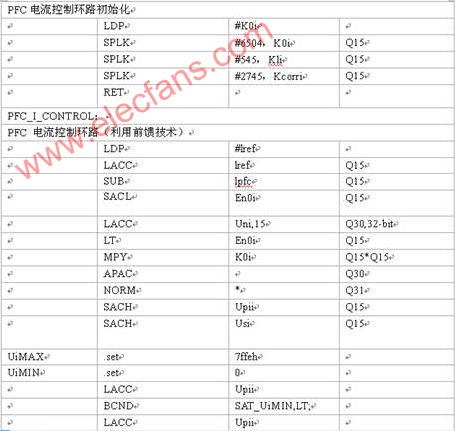
4.2 电压控制器履行例子
PFC变换器负载阻抗为: 。
由于fCV=10Hz,电压控制器量值为GVEA=4.7517。
电压环路PI补偿器零点设置在10Hz,积分时间常数为:T1V=1/2π×10=15.9155×10-3。因此,完整的电压环路控制器为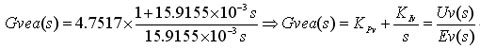
式中,KPV=4.7517,KIV =298.56。
控制器履行等式如下:
Uv(n)=K0v?Ev(n)+Iv(n-1)
Ivi(n)=Iv(n-1)+K1v?Ev(n)+Kcorrv?Epiv
Epiv=Usv-Uv(n)
式中,当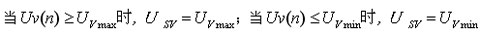
电压控制器的相关系数为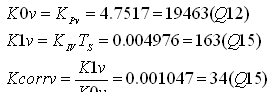
式中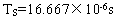 。
。
电压控制器的履行代码段写法与电流控制器相同。
4.3 实验结果
在224Vrms输入电压下的PFC变换器输入电流波形如图5(a)所示,图5(b)所示为在100Vrms输入电压时的输入电流波形。从输入电流波形可以看出,其形状趋于标准正弦波,而且与输入电压趋于同相位,因而实现了功率因数校正。
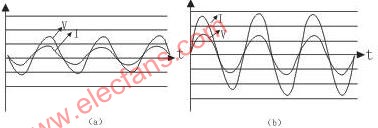
图5 输入电流和电压波形(a)224V输入;(b)100V输入
5、结束语
采用DSP的PFC变换器设计不同于传统模拟控制设计方案,不同控制环路参数必须从模拟控制重新定义到它们的数字的履行,许多具有模拟控制经验的工程师为适应从模拟到数字环境的转变面临新的挑战。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)