
1 首先,无限增益多路反馈有源滤波器与Butterworth,chebyshev,bessel,ellipse等不属于同一范畴的概念,无限增益多路反馈只是有源滤波器总多拓扑结构中一种,其他还有Sallen-key、状态变量滤波器、双二阶滤波器等;而Butterworth,chebyshev,bessel,ellipse是实际滤波器逼近理想滤波器的几种近似算法,有无限增益多路反馈Butterworth滤波器或无限增益多路反馈chebyshev滤波器……
所以,要是比较的话,也是无限增益多路反馈与Sallen-key、状态变量滤波器、双二阶滤波器等拓扑结构相比较;或者,Butterworth,chebyshev,bessel,ellipse几种近似方法相比较。
2 曾经也搞过有源滤波器,也说一下无限增益多路反馈滤波器的优点:返相端输入,失真较小,另外元件灵敏度要求也比Sallen-key低。
四种近似方法的特点:
1、巴特沃斯:通带最大平坦性,但是过渡带衰减不够陡峭,而且其阶跃响应会产生上冲或波动,所以不适用于处理脉冲信号;
2、切比雪夫:通带有起伏,但是过渡带较陡峭,常用于AD转换器前的抗混叠滤波器,阶跃响应同样会产生上冲或波动;
3、椭圆:也有称为考尔滤波器的。通带起伏更大,而且衰减带也有反d,但过渡带最陡峭;
4、贝塞尔:也有称为汤姆逊(Thomson)滤波器的。最大的特点就是阶跃响应的波动最少,所以适用于处理脉冲信号,但是过渡带最不陡峭。
二 无限增益多路反馈有源滤波器设计电路设计总让外人觉得很难,很神秘,其实自己来试一下很简单;
作设计有两步工作要做,其一是测量目标的频率特性和相位特性;然后是设计电路模拟;
下面简单介绍一下频率特性模拟部分的设计;
下图是无限增益多路反馈有源滤波器的基本形式图:
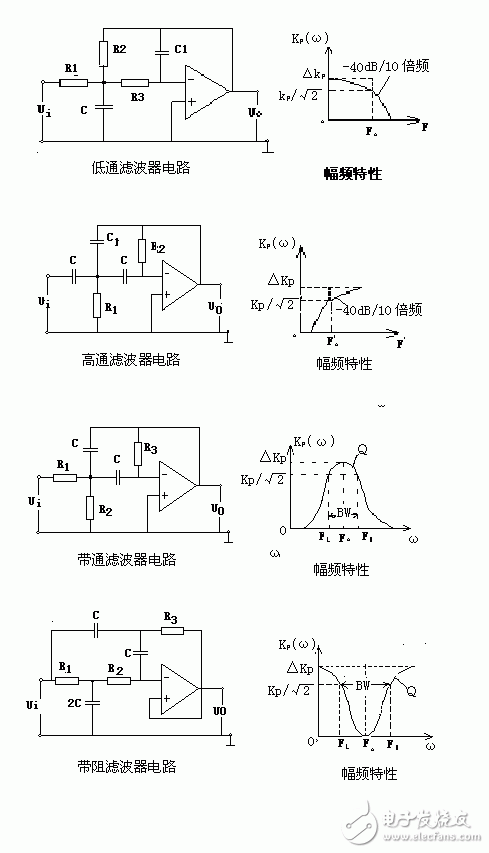
1 要设计RC滤波器,一般采用查表归--快速的设计方法。使用这种方法,必须满足滤波器条件。
首先给定要求的截止频率fc,增益Kp;
选取滤波器的类型(切比雪夫型、巴特沃斯型),(低通、高通、带通、带阻);
选取(一阶、二阶、三阶、四阶、或高阶)滤波器,请参考一些相关资料。《测控电路》、《精密仪器电路》……然后按下述步骤设计:
(1)先选择电容C1的标称值,电容C的初始值靠经验决定,通常以下面的数据作参考:
f c ≤ 100Hz C = (10-0.1) μF
f c = (100-1000)Hz C = (0.1-0.01) μF
f c = (1-10k)Hz C = (0.01-0.001) μF
f c = (10-1000k)Hz C = (1000-100)pF
f c ≥ 100kHz C = (100-10)pF
(2)所选择的电容C1的实际值,再按照下式计算电阻换标系数K
K= 100 /(fc *C1) 其中fc的单位为Hz;C1的单位为μF。
(3)表2-1中查出C1和K=1时的电阻值。
(4)再将这些电阻值靠标称的实际电阻值
2 设计实例
设计一个二阶无限增益多路反馈1dB切比雪夫型低通滤波器,增益Kp = 2,截频(指纹波之间的终止频率)f c = 5KHz。设计步骤如下:
按上述快速设计方法得到标称的电容取C =0.01μF,对应的参数K=2,也可以由式
K= 100 /( f c*C1)= 100/(5000*0.01)=2
从下表中查出Kp=2时,电容C1=C=0.01μF,K=1时的电阻值。
R1=2.602 KΩ
R2=5.204 KΩ
R3=8.839 KΩ
将上述电阻值乘以参数K=2,得:
R1=5.204 KΩ, 取标称值5.1K+104Ω
R2=10.408KΩ, 取标称值10K+408Ω
R3=17.698 KΩ。 取标称值15K+2.7KΩ或≈18K
3 滤波器设计用表

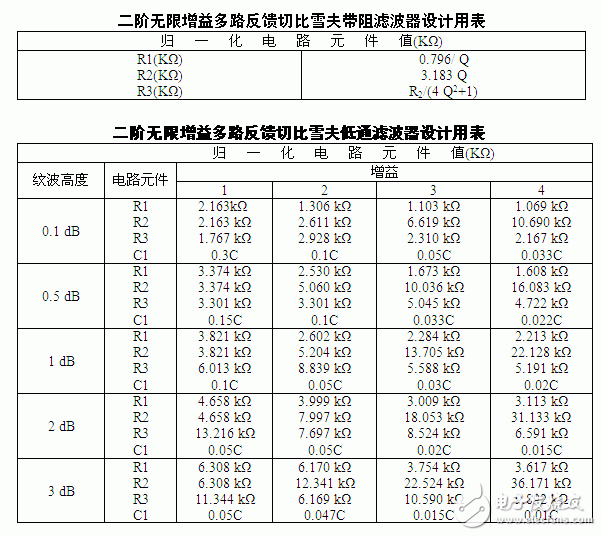
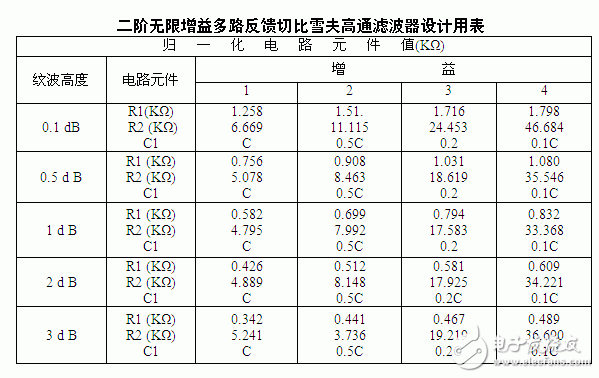
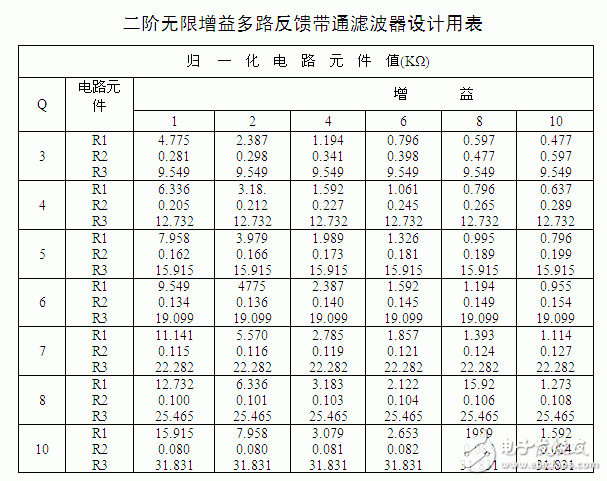
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)