无功补偿容量优化分析

无功补偿是用来提高电压质量、降低网损的有效措施之一，方法是给感性电路中的电感并联电容器，使感性负荷所吸收的无功功率大部分有电容器提供。无功补偿容量的确定有一般方法和优化方法。本文简略分析无功补偿容量的经典优化法。

1 补偿容量优化法

无功补偿容量的优化法是：分别从网损最小、年运行费用最小、年支出费用最小的观点出发，求出最佳补偿容量的算法。这些算法的特点是：求得所要求的量值的数学表达式，然后用求函数极值的方法，求得补偿容量。是一些古典的求极值算法，故称为经典优化法。

1．1 按网损最小确定补偿容量

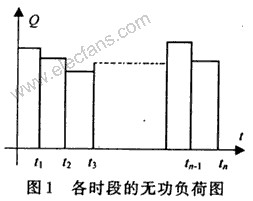
无功补偿的目的是降损节能，因此，从网损最小的观点出发来确定补偿容量是很重要的。如图1所示，该图中各段时间内的总无功负荷为Q，，Q：，…，Q。，假定网络总补偿容量为Q。，则全年的电能损耗和无功负荷的关系为：



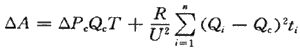
其中：△Pc是补偿电容每Kvar的有功损耗(kW)；T是年运行时间(h)；R是补偿点至电源的等值电阻(Ω)。为使网损最小，可将网损△A对Qc微分，并命其为0，则其：



这种算法比较简单，但没有计人补偿电容所需要的费用。该算法所能保证的只是网损最小，但如果考虑安装补偿电容的费用，不一定是最经济的。

1．2 按年运行费用最小确定补偿容量

年运行费用由两部分组成：第1部分是加装电容器后网络损耗的电价，即F1=△A×β，△A是年电能损耗(kW．h)，β是有功电价[元／(kW．h)]第2部分是补偿装置的年运行、维护费用，即F2=KaKcQc，其中Kc是装设单位补偿容量的综合投资(元／Kvar)，Ka是补偿装置的维护费用率(％)。年运行费用F＝F1十F2=△A ×β十KaKcQc，将△A值代人。为使F最小，将F对Qc微分并命其为0，得：



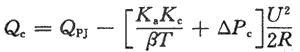
1．3 按年支出费用最小确定补偿容量

年支出费用是指同时考虑年运行费和投资的回收。设投资每元钱的回收率为Ke％，年支出费用为：Z＝F+KeKcQc，其中F是年运行费用；Ke是投资每元钱的回收率。该式采用直线平均法，将电容补偿的总投资平均分摊在各个年度。为使年支出费用最小，将Z对Qc微分并令其为0，从而可求得：



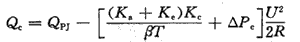
上述3种方法的基本思想和计算公式的形式很相似，但其所计及的因数和获得的经济效益却各不相同，所以其适应的范围也因此而异。通过分析，可见；第1种方法的补偿量和投资均是最大的；第2种方法的补偿量和投资皆居中；第3种方法的补偿量最小，因此其所用的投资也最小。

2 分支线路中补偿容量的最佳分配

在此仍然采用经典优化法。首先求出线路的总损耗△p的表达式，为了使总损耗最小，将△p对分支的补偿容量Qci微分并令其为o，便可求得各分支的最佳补偿容量Qci。

2．1 辐射分支线路中的补偿容量的最佳分配

图2所示的辐射式分支网络中，若其共有n个分支，则装置的总容量Qc在各个分支中应该进行合理分配。总损耗表达式为：



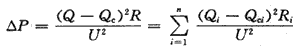
将△p对Qci微分并令其为0，得：

(Q-Qci)Ri＝(Q-Qc)R

其中：Q是网络总无功负荷；Qc是补偿总容量；只是全网等值电阻。从该式可得：



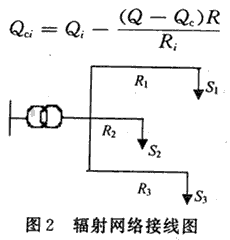
这说明：在辐射分支网络中，当网络无功总负荷Q、总补偿容量Qc及各分支无功Qi为已知的条件下，各分支的补偿容量Qci只取决于全网等效电阻尺和各个分支电阻Ri。

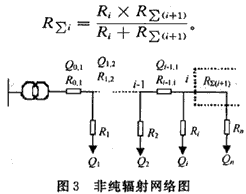
2．2 非纯辐射分支线路中的补偿容量的最佳分配

典型的非纯辐射电网如图3所示，如果要在第i个节点进行补偿，则要对第i一1个节点和i个节点的情况联合考虑。如果第i一1个节点和i个节点之间的无功容量为Qi-1，而节点i一1和i之间的总补偿容量为Qci－1，i，则两者可分别视为节点i之后的总无功需求量和总补偿容量。如此可套用上式，得：



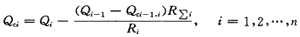
其中：Q是第i个分支的无功负荷(Kvar)，R∑i是第i个节点后网络的等效电阻(Ω)，Ri是第i个分支的电阻(Ω)，而且



3 其 他

用经典优化法，还可计算负荷沿线分布时最佳补偿点的位置和容量配置。其中负荷沿线分布的情况有：均匀分布、递增分布、递减分布、等腰分布等。补偿方式有单点补偿、两点补偿和n点补偿。当无功负荷非均匀分布时，补偿容量用相对分析法来确定。该方法通过引入阻值系数，将非均匀分布负荷化为求解均匀负荷分布的问题，然后用叠加原理，将多电源供点的问题化为单电源供电问题来求解。在此，由于篇幅有限，只能提到而已。