使用PLC来实现闭环控制 选择何种控制方式非常重要

一些闭环运动控制的应用很显然需要运动控制器，然而一些人也可以通过使用PLC来实现闭环控制。当然，选择何种控制方式常常难以定论。

当你可以使用PLC控制的时候，为什么还需要花钱去购买一个专用的电液运动控制器呢？答案很简单。一般来说，考虑的因素包括使用数量，实现难度，可用时间，生产效率，精度要求以及经济性等。做出何种决定往往是很模糊的。根据以往的经验，我知道哪种类型的应用可以用PLC，哪种不适用。

模拟量的反馈必须转化缩放为位置单位。然而，我很奇怪的是，在一些PLC论坛里，很多的人在咨询如何把一个模拟量转化为毫米或英寸。如果编程的工程师在问，很显然他啥也编不了。对输入值比例缩放之后，很简单的做法就是，从指令位置减去实际位置，差值乘以比例增益，该值作为模拟量的输出至阀。就是这么简单！

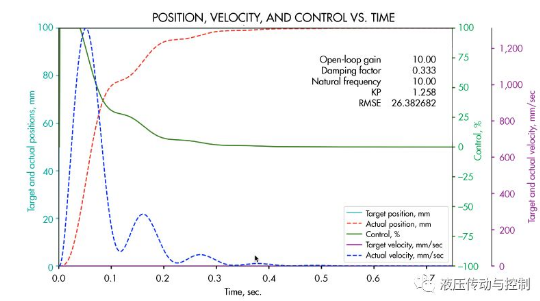
1. 该仿真显示了当指令位置突然改变100mm时将会发生什么。控制输出在100%饱和，执行器突然加速。实际位置则慢慢的接近100mm的目标值。

模拟量控制的PLC设置

PLC控制的一个挑战发生在液压缸的指令和实际位置相差很大的情况，因为此时输出至阀的信号可能很大。结果就是液压缸全速运动至指令位置。在指令位置的时候会发生什么就取决于增益和负载大小了。有时候液压缸会平滑减速至指令位置，但是如果负载很大，也会产生超调，并带有衰减振荡。

关于此问题可以有多种解决方案。一个简单的办法就是限制输出值为低于100%的某个值。更好的解决办法就是准备一个目标发生器，从而可以朝着指令位置的的方向增加目标值。接着，不是比较指令位置与实际位置，而是比较实际位置与下一个目标位置。目标位置在当前位置开始启动，按照期望的速率增加并达到指令位置。对于长行程运动来说，则可以避免初始运动时的振动和冲击。这种解决方案相对来说也比较容易实施。

举个例子，如果两个液压缸跟随同样的目标位置，其位置同步是相对容易的。如果两个缸所受的负载完全一致，目标值的跟踪误差也应该一致，因此它们的实际位置也会非常接近。那么，对于只有比例控制的系统来说，跟踪误差是什么呢？

跟踪误差公式：

Ef = v/（K ？ Kp）

此处：

Ef - 跟踪误差，mm，

v - 速度， mm/s，

K - 开环增益， （mm/s）/%

Kp - 比例增益， %/mm.

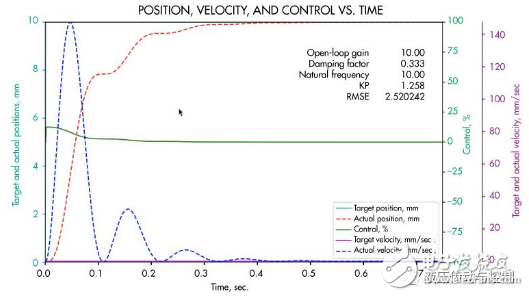
2. 该曲线与图1说设想的方案一样，只是指令位置只改变10mm。注意的是它们用了同样的时间。这是因为运动控制的时间常数是5倍。5倍时间常数即0.358s。意味着1mm的运动要花0.358s才能达到目标值的1%。

单位很重要，并需要保持一致。百分比代表控制输出的百分数。控制输出的百分数可以是 ±10 V， ±20 mA的百分数，或者其它的，只要单位一致就可以。当使用PLC的时候，跟踪误差通常情况并没有那么重要，液压缸只需要能够大体的接近指令位置即可。上面的等式适用于对跟踪误差有限定的应用。用户可以决定动作速度，以满足应用要求。

计算开环增益需要用到VCCM公式，其计算了在100%控制输出时最大的稳态速度。该公式在相关论坛已经讨论过很多次。（延伸阅读：VCCM-如果流量计算不再是Q=A*V？）

比例增益的计算稍微复杂一些。你可以尝试使用试错法，确定一个可以看起来可以工作的数值。如果增益太低，液压缸响应会很迟缓。如果增益太高，执行器会有振荡的可能。然而，最优的增益是可以计算的：

Kp = 2 ？ ζ？ ωn ？ （9 ？ 8 ？ ζ2）/（27 ？ K）

此处：

Kp - 比例增益，输入偏差信号变化的相对值mm与输出信号变化的相对值之比的百分数表示，

ζ - 阻尼系数（未知时假定为0.3333），

ω - 自然频率，弧度/s

K - 开环增益

你也许无法在教科书里找到比例增益公式推导的来源。然而，液压系统设计工程师实际上知道如何控制最优的比例增益，因为他们必须确定阻尼系数，自然频率以及开环增益。通常，自然频率是根据油液的体积d性模量，液压缸作用面积，油液压缩量，质量等计算而来。因为跟踪误差取决于开环增益和比例增益，液压设计者必须控制跟踪误差。

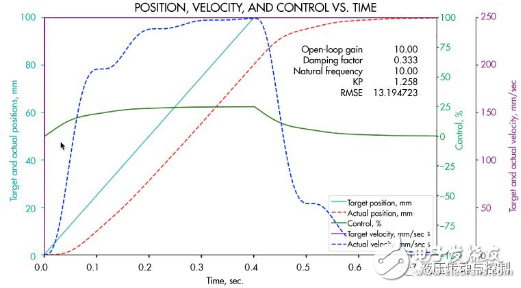
3.该仿真显示了添加一个简单的目标发生器所带来的好处。需要注意的是控制输出并不饱和，实际位置移动更平滑。速度达到期望值的250mm/s（100mm/0.4s）。加速度小很多。速度比例与第1和第3个仿真有很大不同。

对于比例控制的其它思考

假如控制系统已经调定好，并开始一段短行程的运动，并工作起来似乎很正常。试图运动更长一点的距离，两次运动消耗几乎相同的时间。原因就在于随着误差减小，控制输出也减小，因此速度也会大幅减小。对于实际的位置，如果减小的误差低于原始误差1%，其将消耗5倍的时间常数。

时间常数就是控制对象减小63%的错误所用的时间。因此，如果误差迅速上升10mm，而时间常数是1s，误差将在1s之后降至3.68mm。2s之后，误差将降至1.35mm。在5倍的时间常数（5s）之后，误差将减小至0.067mm-低于原始误差10mm的1%。时间常数决定了控制系统将要花多少时间来响应系统的干扰。

现在问题就是，对于一个仅仅采用比例增益的液压缸，如何计算其时间常数？公司并不难：

τ 是最优时间常数。

τ = 3/（2 ？ ζ？ ωn ）

如果阻尼是0.33333，自然频率是10Hz，则时间常数是：

τ = 3/（2 ？ 0.333 ？ 2 ？ π ？ 10） = 0.072 s.

因为其消耗5倍的时间常数以达到减小误差至1%，运动过程则将需要0.358s。

需要再次注意的是，最优的时间常数完全由机械（液压）设计者来决定。5倍时间常数的时间过长，液压系统设计者就需要考虑提高自然频率，或者通过增加摩擦提高阻尼。增加摩擦浪费能源。提高自然频率需要增加液压缸缸径，而且也会增大阀通径，蓄能器容积，泵能力以及增加的元件成本。

采用带PLC的简单的比例控制液压系统似乎容易得多，但是PLC编程人员对很多重要的参数并没有去控制。这种约束并不是编程人员的能力问题，而是液压和机械设计方面的原因。不幸的是，PLC编程人员通常是最后一个接触到液压系统的人，他被寄希望于“机械和液压问题，让电气和软件来解决”，然而，这种事实，不会总是发生。系统的特性行为在设计和制造阶段已经定性了。

设备的性能可以通过使用精密的液压伺服控制系统得到提高。初始的成本会很高，但是其性能也提升了。设备也变得易于维护，需要的维护频率也不高了。

下面是仅仅采用比例控制的简单运动的三种仿真。它们基于标准的线性化运动仿真模块，用于伺服液压缸和负载。

H（s） = （K ？ ω2n）/［s ？ （s2 + 2 ？ ζ ？ ωn ？ s + ω2n）］

K，- 开环增益，假定为10 （mm/s）/%的控制输出，

s， - 拉普拉斯算子，是一个频率，弧度/s，

ζ - 阻尼系数，假定为0.33333，无量纲，

ωn - 自然频率，弧度/s。示例中自然频率为10Hz。