基于PDM的DA转换技术

　　1 引言

　　在数字信号处理中，常常需要将多位数字信号转化为一位数字信号。例如，在通信领域，接收器接收到经过编码的数字语音信号，需将他转化为模拟信号，即将原来的模拟语音信号复原。经过编码的语音信号，通常是多位的比特流。因此，如何将多位比特流转化为模拟语音信号，便成为保证通信质量的关键。又如，在一些控制电路中，控制信号是经过计算生成的多位数字信号，而这些数字信号必须转化为模拟信号才能对电路进行控制。因此，如何将多位数字信号转化为符合实际要求的模拟信号，则成为控制电路设计者最关心的问题。

　　在传统的电路设计中，面对上述问题时，通常选择使用由多个分离的电子元器件组成的D/A转换器，有时我们也称他为静态D/A转换器。但是由于静态D/A转换器的组成结构，决定了他在系统中，必须占用一定的空间及消耗一定量的功率。于是在那些要求携带方便的系统方案中，静态D/A转换器就不得不被替换掉[1]。

　　于是人们选择所谓“数字基础”的D/A转换器。而用于数字D/A转换的方法有2种：PWM(P ulse Width ModulaTIon)脉冲宽度调制和PDM(Pulse Density ModulaTIon)脉冲密度调制。这种数字D/A转换器所占用的物理空间比较小，消耗的功率也比较小。因此，适用于对系统硬件大小以及功耗要求比较严格的系统[1]。

　　早在20世纪40年代，PWM就开始被应用在电话中。由于PWM的局限性，人们在二十年后，提出了PDM调制方法。但由于当时的应用市场尚不成规模，因而这种调制方法一直未能得到广泛的关注和应用。近年来，由于数字技术在各个领域里得到了广泛的应用，数字产品飞速发展，数字信号处理开始得到越来越多的关注。于是PDM调制技术重新得到重视，并被应用在不同的领域中。

　　2 PDM基本介绍

　　PDM是一种在数字领域提供模拟信号的调制方法。在PDM信号中，逻辑“1”表示单个脉冲，逻辑“0”表示没有脉冲。通常逻辑“1”和逻辑“0”是不连续的，逻辑“1”比较均匀地分布在每个调制信号周期里。其中单个脉冲并不表示幅值，而一系列脉冲的密度才对应于模拟信号中的幅值。完全由“1”组成的PDM信号对应于幅值为正的电压;而完全由“0”组成的PDM信号则对应于负幅值的电压;由“1”和“0”交替组成的信号则对应于0幅值的电压。

　　3 PDM的实现

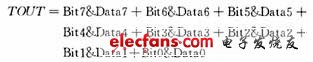
　　PDM调制技术的逻辑框图如图1所示。用1个分频计数器实现符合实际应用要求的时钟信号，脉冲周期为ΔT.再将时钟信号送入　N位计数器，实现0，1，…，2N-1的计数。在计数的单个脉冲周期ΔT里，将计数结果各个位上的逻辑值经过一系列逻辑 *** 作，实现N位比较基准脉冲信号，分别为Bit0，Bit1，Bit2，…，Bit(N -1)。值得注意的是，在每一个ΔT里，都只有一个位上有逻辑“1”，其他位 上均为逻辑“0”。同时将寄存器输出的N位总线数据与比较基准脉冲信号Bit0，Bit1，Bit2，…，Bit(N-1)进行逐位与 *** 作，再将各个位上的结果相或，便得到ΔT内的调 制结果。这样，在整个调 制周期结束后便得到调制结果。

　　对于N位的数字信号，调制周期T=2N.ΔT.对于8位的数字待调信号，每个脉冲周期ΔT的调制结果为：

　　例如，对8位的十六进制数字信号“1AH”进行调制。用8位的计数器产生如图2所示的比较基准脉冲信号。显然，在每一个脉冲周期ΔT里，Bit0~Bit7中都只有1个位上有脉冲。

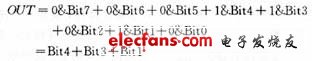
　　而十六进制数“1AH”对应的二进制数为“00011010”，其中Bit4，Bit3，Bit1为“1”，其他各位均为“0”，经过逐位逻辑 *** 作，即：

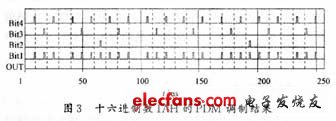
　　经过一个调制周期的调制，便得到如图3所示的调制信号。这样8位的数字信号就转化为1位的脉冲信号。