staking已成为区块链发展史上的重大变革

一、时间跳跃的分歧

staking毫无疑问名列今年最火爆的概念。眼下，越来越多的人争相恐后参与其中。

作为PoS机制下的挖矿手段，相比起比特币等PoW机制，staking不用耗费大量的算力资源，持币人只需将币暂时质押给节点，就能在一段时间内与节点一起分享出块或验证区块得到的奖励。

不少乐观者认为，熊市暴露了PoW机制的弊端，而staking受熊市影响会更小，因此更安全；有人认为，staking近似于一种理财产品，会给大家带来稳定的分红；还有人认为，可以把staking看做一种治理行为，帮助更多用户参与到社区治理中来。

当然，staking也并非完美。有人提出疑问，在一些设计下，它可能导致高通胀，导致参与者赚币亏钱，还有的人套用互联网模式补贴思维，通过烧钱补贴恶性竞争，为经济生态安全埋下隐患。

本次Trias发布的staking方案设计，希望每一个关注Trias的小伙伴都能一同加入进来，留下自己宝贵的建议，大家在讨论中的遇到的各种问题和改进方向，我们都会尽量以社区方式去解决。

二、开始与结束的规则

前文中，我们介绍道，Trias的经济生态整体共有三层（Leviatom、Prometh、MagCarta），此文的设计仅为最上层的应用层，也就是MagCarta层的经济设计。

我们发现，对一些staking项目而言，之所以会引发通货膨胀，是因为其通货膨胀百分比是纯粹由炒作决定的。要解决这个问题，我们认为新生成的代币应该与链上活动及生产力密切相关，即staking回报比例应与实际经济产出成正比。

为贯彻我们的信念，我们创建了一个分红池，来为企业提供回报。这样一来，池中代币的数量就能很好地反映出DSaaS应用中的经济产出。在分红过程中，倘若没有新生成的代币，分发给奖励则来自于市场流通，并逐渐流向开源社区。

我们认为这个方法能够有效的控制现在市面上进行staking时出现的通货膨胀问题。而这个staking与DSaaS相结合的核心理念，我们称之为“效率通货膨胀映射”。

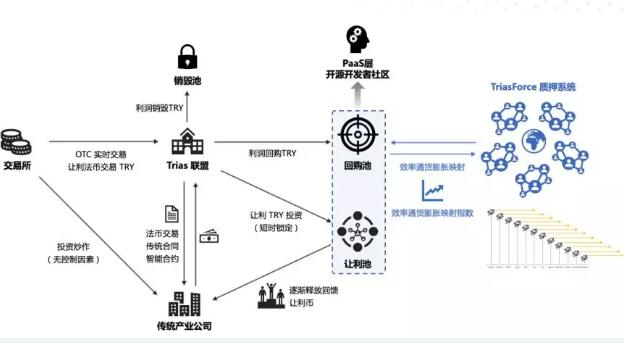
效率通货膨胀映射定义：

在一段时间内（如t0-t1）累计流入分红池的总代币数量s被记录下来。根据效率通货膨胀映射产生一个指定的staking池子。此池子代表t0到t1的表现，效率通货膨胀映射指数为θ。此池子的staking奖励代币为sθ。

三、梦幻相生的平衡

这里我先对上面的定义加以分析。举一个例子，比如2019年1月1日到3月1日，累计共有1000个TRY代币流入分红池。那么分红池会通过映射形成一个staking池，如效率通货膨胀指数为5，那么此staking池的总代币奖励就是5*1000=5000个。

在Trias系统中，存着着很多这样staking池子。这些池子会随着传统经济中的企业周期而变化。作为staking奖励，每个staking池子里的新生代币对应的是这段时间内分红池内的积累。

staking 奖励的回报率可以从此公式中得出：

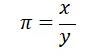
其中，X=staking池子的代币奖励，（就是分红池单位时间内累计流入代币*效率通货膨胀指数），Y=一个池子staking的代币。

X来自池子里的代币奖励，π有Trias系统决定。重点来了，staking池子里的奖励只对抢购成功者进行回报，而非所有持币人，综上我们可知，最终回报数量为X+Y。

再举一个例子。如果X依然是5000个，并且系统将回报率定为50%，则Y为5000/50%=10000个。在一个staking池的锁定期结束后，所有抢购成功者可获得5000+10000=15000的TRY奖励。

为示公平，我们使用拍卖（AucTIon）来允许参与者抢在一个staking池子里的的权利。

四、穿越时空的控制

当然，拍卖也好，抢购也好，都要在一定的规则下进行。这个规则涉及到时间和空间两个层面。

从时间来看，每个AucTIon从开始到结束时的单位时间结束后，池子会立刻关闭。并根据公式计算出回报率π。

从空间来讲，倘若staking在抢购时间未到额定时间即达到Y的最大值，那么池子同样会自动关闭。

换言之，时间限制和Y的极值限制，都是池子关闭的充分条件。

这套机制在实践应用上已经被证明对整体通胀影响很小而且是在控范围之内的。举一个例子，8月1日8点，Trias通过回购1000000个TRY，并开启池子staking以回馈某省电力产业企业客户，回报率π设置为15%。持续时间1个小时，此时间内，持币者可以随时进行stake，当回报率触碰到15%时候，或直到额定的1小时时间，staking aucTIon结束。

这个设计不但确保了参与者可以充分得到奖励，还保证了市场不会在某个时间承受极大的抛压，维护了Trias经济生态的稳定。

关于staking的研究还在继续中，这块富饶的金矿目前仍然没有完全释放其价值。惟其如此，staking以其独特的魅力，未来仍将吸引更多人贡献自己的聪明才智，逐步探索其最完美的实现方案。