椭圆曲线并行加速的研究与讨论

2019年4月19日，第十四期北大软微-八分量协同实验室学术沙龙活动如期展开。本次技术沙龙围绕着椭圆曲线并行加速的研究展开讨论。北京大学的沈晴霓教授、方跃坚副教授、Trias胡志琳以及软微学院众位博士生、硕士生参与了此次沙龙，并由方跃坚老师和博士生冯新宇做出分享。

此前我们提到，同 RSA 公钥密码相比，椭圆曲线密码提供了更高的单位比特安全强度 ， 160 位密钥长度的椭圆曲线密码提供的安全强度，相当于 1024 位密钥长度的 RSA 密码提供的安全强度。在这种背景下，对运算进行优化便具有重要意义，并行加速便是优化运算的一种方式。

椭圆曲线加密的并行性处理方式到目前尚在学术界讨论阶段，是一个比较前沿的研究方向。就目前从技术角度而言，并行性存在着安全隐患和效率提升不明显等问题，所以这项技术尚未大规模落地投入应用。即便是以比特币为代表的加密货币这样的轻量级应用，出于种种顾虑，也未采用并行加速。

方跃坚老师首先提出4种可能提升椭圆加密算法效率的方式，分别是多线程并行、GPU并行、专用硬件并行处理器、SSE指令加速。方老师在介绍这4种方法之余，还从不同角度比较了他们相互的优劣，如GPU并行虽然单位时间内总吞吐量较高，但单个运算却不如CPU；专用硬件虽然能较为容易的将点乘转化为点加提升速度，在抗攻击等方面则存在一些问题。

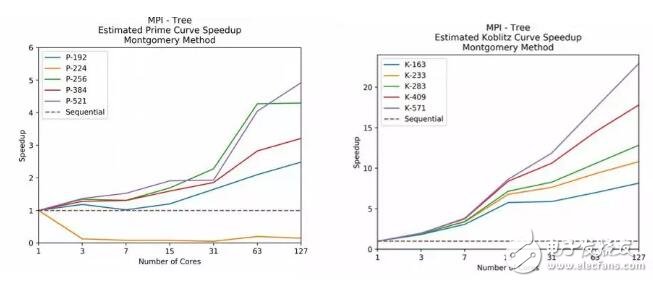
博士生冯新宇则相对详细的从不同的论文中筛选出几种可能会提高效率的算法。它们都是从一个等式出发：Q=KP。在这个等式中，K是一个大整数，P相当于私钥，Q相当于公钥，所有这些算法都是通过对整数K进行转化来减少点运算的次数。想要提升效率，就要找到一个快速计算出K·P结果的办法，既然P不能变，那就只能从K来入手。

下面是冯博对这些算法逐一做出简述：

二进制算法：将K转换成2进制（即2的幂）的形式，然后再进行背点运算和点加运算，时常和滑动窗口方法结合起来使用。

窗口NAF方法：通过编码来减少比特位中含1的个数，从而减少点加的次数。但是有一个缺点，即不能抗边信道攻击。

边信道攻击（SCA， Side Channel Attack）是一种通过分析密码设备泄露的边信道信息来推测秘钥的密码分析方法。

滑动窗口方法：通过跳过比特值为0的位来减少点加的次数。

Montgomery：Montgomery 型椭圆曲线定义为E ：By2 =x3 +Ax2 +x。此处 ， A ， B ∈ Fpn并且B（A2 -4）≠0。Euclid 加法链是满足如下条件的加法链 ：v1 =1 ， v2=2 ， v3 =v1 +v2，对所有的 3 ≤i ≤l -1 ，如果 vi =vi -1 +vj（j 《i -1），则 vi +1 =vi +vi -1或 vi +1 =vi +vj。通过辗转相减可以求得计算任意整数 k 的加法链，但该加法链的长度取决于选取的减数g ，求最短加法链问题是一个 NP 完全问题。

NP完全问题，是世界七大数学难题之一。NP的英文全称是Non-determinisTIc Polynomial的问题，即多项式复杂程度的非确定性问题。简单的写法是 NP=P？，问题就在这个问号上，到底是NP等于P，还是NP不等于P。

固定窗口方法：预存P的i倍来减少点加次数。这种方法很容易理解，即将几种可能的情况提前算好，使用的时候直接拿来取用，提升效率的办法。

沈老师提出了一些问题，如加密签名验证等繁琐的工作能否交给架构，而非用户来处理，并行性能否做出多机分布式等，交给大家集思广益，作为以后讨论的方向。最后，除了在硬件上入手外，大家总结了一下提速的两个大方向，一是优化算法，二是拆分多线程。