电源DCDC模块输入滤波器的设计

　　无阻尼LC滤波器

　　图1所示为无阻尼LC无源滤波器。理想情况下，一个二阶滤波器在谐振频率f0后每倍频衰减12dB。其在f0之前没有增益，在谐振频率f0处增益达到峰值。

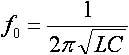　　 （1）

　　

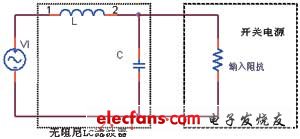
　　图1 无阻尼LC滤波器

　　二阶滤波器在设计上的一个关键因素是频率f0处的衰减特性。谐振频率处的增益非常大，同时也放大了该频率处的噪声。通过分析滤波器的传递函数可以更好地理解问题的本质。其传递函数为

　　（2）

　　传递函数也可用弧度来表示：

　　 （3）

　　其中，，以弧度表示的谐振频率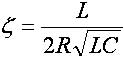；是阻尼因子。

　　该传递函数有两个负的极点和，阻尼因子ζ表示该角频率处的增益。当ζ《1时，两极点为复数，虚部使增益在谐振频率处达到峰值。

　　

　　图2 不同阻尼因子时LC滤波器的传递函数

　　阻尼因子越小，谐振频率处增益越大，达到理想零阻尼时增益为无穷大。然而，元器件的内阻限制了增益达到最大值。在此，阻尼因子就像一个虚拟元件，妨碍增益达到峰值。

　　在输入滤波器设计中，阻尼因子和系统性能关系很大，阻尼因子会影响反馈控制回路的传递函数，也会在开关电源输出端引起振荡。

　　Middlebrook附加元素法则指出：如果输入滤波器的输出阻抗曲线远低于变换器的输入阻抗曲线，输入滤波器就不能明显改变变换器的闭环增益。换句话说，保持滤波器的输出阻抗峰值低于变换器的输入阻抗非常重要，因为这样能避免产生振荡（见图3）。

　　

　　图3 滤波器输出阻抗和开关电源输入阻抗

　　从设计观点上，根据阻尼因子最小值的1/√2倍（此时，谐振频率处增益衰减3dB），获得最佳的滤波器性能体积比，使控制系统达到良好的稳定性。

　　并联阻尼滤波器

　　在大多数情况下，图1中的无阻尼二阶滤波器不易满足衰减要求，于是考虑选择阻尼滤波器。

　　图4所示的阻尼滤波器由电阻Rd和电容Cd先串联再与滤波器电容C并联构成。电阻Rd的作用是降低滤波器在谐振频率处的输出阻抗峰值；电容Cd抑制输入电压的直流成分，防止Rd消耗功率。

　　

　　图4 并联阻尼滤波器

　　为了不影响LC主滤波器的谐振频率，电容Cd在谐振频率处的阻抗应小于Rd，且比滤波器的电容值要大。

　　滤波器的输出阻抗可根据三个并联的方框阻抗来计算：

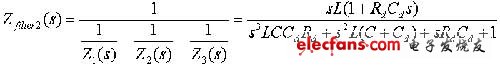　　（4）

　　传递函数为

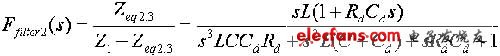　　（5）

　　此处，Zeq2.3为Z2和Z3并联值。传递函数上有一个零点和三个极点，零点和第一个极点非常接近地位于频率ω≈1/RdCd处，另两个主极点落在谐振频率处。近似计算中，零点和第一个极点可以忽略不计，则此公式近似表达了一个二阶滤波器（当频率大于ω≈1/RdCd时，（1+RdCds）≈RdCds））。

　　（6）

　　并联阻尼滤波器的近似计算公式和无阻尼滤波器的传递函数相同，唯一区别是阻尼因子ζ的计算要加上电阻Rd。

　　图5和图6分别为并联阻尼滤波器的输出阻抗和传递函数。

　　

　　图5 并联阻尼滤波器输出阻抗

　　

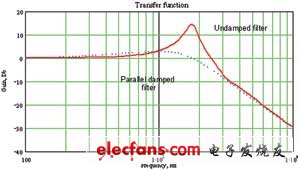
　　图6 并联阻尼滤波器传递函数