如何估计电源管理IC的连接线载流能力

　　连接线广泛用于连接芯片的引线端子和半导体器件的外部引脚。连接所用导线一般由黄金制成，因为黄金能抵御氧化，并具备很高的导电性，而且用黄金可相对容易地连接IC引线端子和器件引脚。

　　用铜导线取代黄金导线的方法势头越来越强，因为铜具备卓越的电气和热特性、相对更少的金属间化合生长和更高的机械稳定性。

　　在电源管理IC等具备大DC电流的器件中，会使用大量导线来传导这种电流。这些额外的导线有助于改善DC压降性能，并降低由大电流及其产生的有关热量（焦耳生热现象）导致的导线熔断或融化风险。不幸的是，就给定应用而言，还没有一种能用来估计导线数量和尺寸的方法或分析方法。所使用的导线数量或者太多，增加了芯片面积和成本，或者太少，导致可靠性风险和器件失灵。

　　本文探讨一种方法，用来估计不同尺寸和类型的导线处理DC电流的能力。本文还提供一些指导原则，将有助于产品设计师估计特定的应用所需的最佳导线数量。

　　估计理论上的载流能力

　　导线熔断的经典设计方程是由W.H. 普里斯推导出来的（1884年，称为普里斯方程），仅适用于在自由空气中的导线。

　　该方程揭示了熔断电流（以安培为单位）和导线直径（以英寸）为单位之间的关系，如下所示。

　　i=kD3/2

　　其中，i是DC或RMS电流；k是常数，其值取决于导线材料，就黄金和铜导线而言，k=10，244；D=导线直径（单位为英寸）。

　　这个方程的限制是，它仅适用于在自由空气中的导线。此外，它未考虑导体长度。而导线的载流能力是受长度影响的，而且会随着长度增加而降低。

　　经过修改的普里斯方程

　　为了解决上述限制，人们对普里斯方程进行了修改，用数值更大的常数k来反映典型应用的情况，在典型应用中，导线是用基于环氧树脂的模塑化合物密封的。这个常数k也反映了导线长度对导线载流能力的影响。导体长度≤0.040”时，黄金和铜导线的k值均为30，000，而在导体长度》 0.040”时，其k值均为20，500。

　　军用规格（MIL-M-38510J）中提到的方程就是基于修改过的普里斯方程。

　　表1列出了用两个版本的普里斯方程计算出的两种类型导体的载流能力。

　　

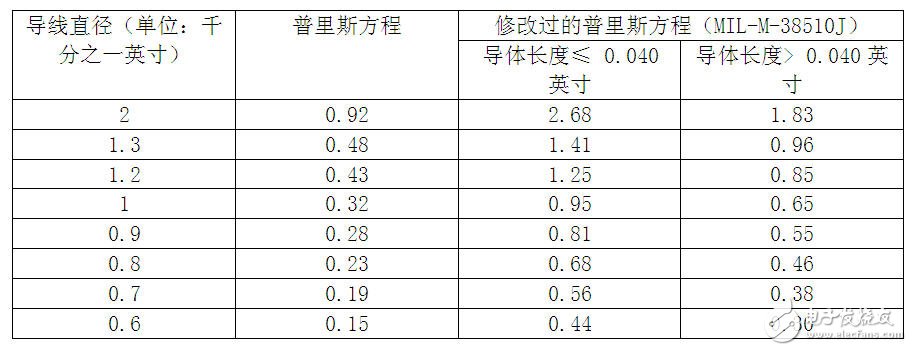
　　表1 基于普里斯方程计算出的载流能力

　　即使是修改过的普里斯方程，仍然存在限制：

　　1所显示的载流能力值是与材料无关的。与黄金导线相比，铜导线的热导率高20%，电导率高30%，这从理论上应该转化为，铜导线能比黄金导线传送更大的电流。

　　2 该方程没有推断导体长度超出0.040”（约为1mm导线长度）时导体的载流能力。大多数应用的导线长度在2～3mm范围内，有时还会超出这一范围。随着导体长度的变化，导线的载流能力有很多的变化，而该方程没有考虑这种情况。

　　鉴于上述限制，有必要寻找一种新的方法，这种方法须考虑已知几何尺寸及材料特性信息以及典型应用造成的限制。

　　导体中的焦耳生热现象

　　当电流流经一段非理想的、具备有限电阻的导体时，就会有热量释放出来，通过称为焦耳生热或电阻生热的过程，将电能转化成热能。所释放的热量大小与通过导体的电流的平方以及导体的电阻成正比，3者关系如下：

　　Qgenerated=I2R

　　就一段被静止空气包围的导体而言，产生的所有热量都通过导体散出，而没有热量从导体表面传导出去。当以下等式成立时，系统达到稳定状态：

　　Qgenerated=Qdissipated

　　通过由以下等式显示的简单热量传导过程，所产生的热量通过这段导线散出：

　　Qdissipated=kAdt/dx

　　其中，k是导线的热传导率；A=导线的横截面积；dT=导线两端的温度差；dx=导线长度。

　　重新排列上述等式并简化为：

　　

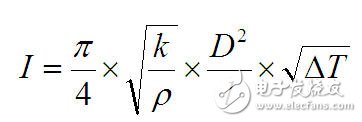
　　进行进一步简化：

　　

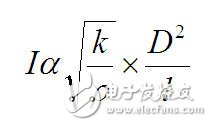
　　根据上述关系，假定其他所有条件都保持相同，那么与黄金导线相比，铜导线能处理的DC或RMS电流应该大25%。

　　在大多数实际应用中，热量不仅能通过导线传导出去，而且还能通过环氧树脂模塑化合物，从导线表面在径向方向传导出去。二者结合以后的热传导现象很复杂，不可能用闭环的方程准确分析。因此，人们运用具备热电耦合物理求解程序的有限的元件建模软件来分析不同导线参数的作用。