开关电源的特点与拓扑结构_技术

前面讲了一些线性稳压的原理和设计的基本方法，事实上，除了一些功率较大或者对精度要求较高的电源设计，使用集成的线性稳压芯片很少出现“翻车”事故，一般只需关注输入输出范围即可。此外，需注意由于集成的开关电源芯片(尤其是贴片封装的，如SOT-223)，由于体积较小，散热较差，一般工作电流在300mA时已经较烫，500mA以上应考虑加散热片辅助散热。

总的来说线性稳压电源设计较为简单，本文开始总结一些开关电源相关的原理和设计方法。

文章目录

开关电源的特点
开关电源拓扑结构
Buck拓扑结构
Boost拓扑结构
Buck&Boost拓扑结构

开关电源的特点

开关电源正如其“名”，其利用半导体管的“开”和“关”实现对控制的输出，由于半导体工艺的进步，半导体管已经能承受较大的电流，并且内阻极小，一般可小于20mΩ，因此开关电源输出能力较强，且效率极高。但同时因其开关特性，其输出不可避免的引入了与工作频率同频率的纹波及其高次谐波，因此一般用于功率较高但对精度要求不高的电路，且若与对精度要求较高的模拟电路之间需要单点接地以消除干扰。

开关电源拓扑结构

常见的DC-DC变换器拓扑结构有Buck、Boost、Buck-Boost、Cuk、Zzeta、Sepic等几种，其中最为常用的是前三种，后面会以Buck电路为例重点介绍。

开关电源的分析计算一般是基于对电感的伏秒平衡关系分析，下面举例说明三种最常用的开关电源结构。需要注意的是，这里仅为了说明原理，实际应用中由于效率、成本等因素的影响结构会有所不同。

Buck拓扑结构

上图为Buck电路的基本拓扑结构，首先感性认知一下，由PWM控制的NMOS管不断的开关，当Q1导通时，输入电压经过电感L1给电容C1充电，由于“电感电流不突变，电容电压不突变”的特性，输出电压逐渐上升，在尚未上升到输入电压时Q1截止，此时LCD构成新的回路，由于电感的“续流”和电容持续提供能量，输出电压逐渐下降。Q1不断开关，重复上述过程，最终输出电压在一个较小的范围内波动。

下面进行计算分析，假设上述控制Q1开关的PWM信号占空比为D，频率为f，则

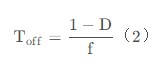
根据伏秒平衡可得

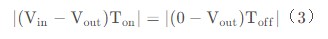
化简得

此时计算得到的即为指定输入和输出时候的占空比，当然上述计算都是有一个假设前提，即电路效率为100%，实际上有损耗占空比会略高于理论值，同时实际运用中很难有一个稳定输入的电源，比如使用电池供电，随着电能的消耗，电池实际输出电压会降低，因此实际使用中需利用实际输出电压反馈来调整占空比。

如图为Buck拓扑结构的mulTIsim仿真，黄色为输出电压，红色为输出电流(1mV/mA)，以函数发生器提供PWM(10kHz，50%，3.3V)，输入电压8.4V(模拟的是2s锂电池)，根据公式(4)可得理论输出电压为4.2V，但从图中可以看出，实际输出电压仅为约5.4mV，这是因为PWM电压仅为3.3V，不能使MOSFET完全导通，实际上欲使MOSFET完全导通需要的电压一般高于整个开关电源的输入电压(早期的开关电源多使用三极管，此时更好理解，欲使三极管工作在饱和区，控制信号所在的基极电压需大于电源输入端所在的集电极)，而要产生这样一个电压大于输入电压的控制信号是非常困难的，实际上控制信号一般为3.3V或者5V，后续的博文在讲述实际使用的Buck电路结构时将详细说明该问题的解决方案(剧透一下~一个自举电容就能解决问题)。

这里暂时以提高PWM的方法代替，得到如图所示仿真结果，可以看到实际输出确为4.2V左右，同时输出电压有明显的周期性波动，该周期性波动的频率即为控制信号频率，波动大小与LC的参数有关。实际上PWM控制开关管输出的是一个有效值为目标输出的方波，经过LC滤波器滤除交流部分得到输出基本稳定的直流电源。

上图红色曲线为电流曲线，可以看到电流是连续的，也就是说每次开关电感都没有完全放电，这种开关模式被称为连续导通模式(CCM，ConTInuous ConducTIon Mode);与之相对的是断续导通模式(DCM，DisconTInous Conduction Mode)，其在每个周期电感完全放电，也就是说其在一个周期内存在输出电压为“0”的情况;另外还有一种介于两者之间的临界模式(Boundary Conduction Mode)，但这是一种非标准的设计模式。

Boost拓扑结构