SiC半导体的热稳定性

众所周知，作为温度函数的传统半导体（Si、Ge 等）的带隙εg遵循以下定律：

其中T 0 = 300 K，a 》 0 是一个系数，其值使得ε g 的变化对于设备的适当工作范围可以忽略不计。

在这项研究中，我们将解释在一定温度范围内对碳化硅样品进行的本征电导率测量

表明对于这个范围（比传统半导体宽得多），带隙实际上是恒定的。这种情况对于器件的热稳定性至关重要。

实验室经验

在我们的研究中，实验室经验包括测量电导率作为数量的函数：

进行测量的半导体样品可以是本征的和外征的（即掺杂的）。在后一种情况下，需要参考本征电导率占主导地位的温度范围，因此从现在开始，我们将采用符号σ intr 来表示电导率。

在室温下，它是

进行测量以将温度升高到最大值

对应于大约 300 ◦ C。因此，变量β 的范围为

然后，我们在对数尺度上报告σ intr 作为β的函数，获得线性下降趋势。所以我们会写：

式中，α 》 0 为排列实验数据的直线原点的纵坐标，χ 》 0 为角度系数的绝对值，如图 1 所示。

从公式 7 可以得出：

其中A = e α 是具有电导率维度的正常数，而χ具有能量维度，因为指数参数是无量纲的。在这个指数中，我们认识了同名统计量的玻尔兹曼因子。

图 1：电导率测量趋势。在横坐标上，数量β = （ k T -1

数据围绕通过插值获得的直线分布。在室温下，它是σ intr （ β 0 ） = 2 。02 米/米。

实验数据解读

在任何理论模型中，半导体的电导率σ很容易从 Drude 模型的扩展中获得，众所周知，该模型调节金属中的电子电导率（然而，没有考虑量子效应）。更准确地说，在半导体的情况下，得到

其中 e = 1 。602·10 -19 C是电子电荷的绝对值；n、p分别为导带电子数密度和价带空穴数密度；µ e 、µ h分别是电子和空穴的迁移率（每单位电场的漂移速度）。对于室温下的 SiC：

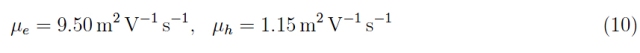
这些量与带隙宽度成反比；这是一个物理上显而易见的结果 ［1］。

考虑到电子和空穴的微观动力学［2］，我们可以写：

带星号的数量分别是电子和空穴的有效质量。我们很快回忆起，这些值测量的是自由粒子在位于 SiC（或任何其他固体、导体/半导体）晶格位置的正离子施加的势能（周期性）能量后与惯性质量的偏差。 。 简而言之，质量为m的粒子在空间坐标中的周期性势能场中的运动等价于不受力但有效质量为m ∗的粒子的运动。剩余量τ e ， τ h 是特征时间间隔（弛豫时间），其倒数是电子-离子（或空穴-离子）碰撞的平均频率。现在我们需要确定电子和空穴的浓度，即数量n，p。作为费米子，我们有单个粒子的能级是根据费米-狄拉克统计来填充的：

其中µ （ T ） 是费米子的化学势。准确地说，当ε ≥ ε C和ε ≤ ε V时，单个粒子的能级连续分布1，即ε C和ε V分别是导带的最小能量和价带的最大能量。形式上，我们可以考虑能级的连续分布：

如图 2 所示。

图 2：半导体的价带和导带示意图，由禁带隔开

它遵循电子

函数g C （ ε ） 是状态的密度，即g C （ ε ） dε是之间的能量状态数

ε和ε + dε是量子典型能级退化的连续模拟

系统。从［1］：

所以

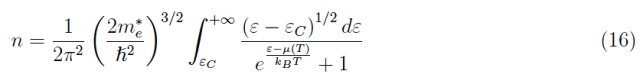
同样对于孔

根据洞的定义：

在统计描述中（因此是大量粒子的行为），量化水平的分布非常密集，因此可以很好地近似于连续谱。

和

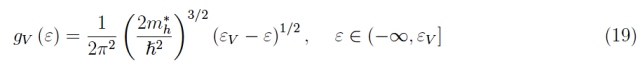
所以

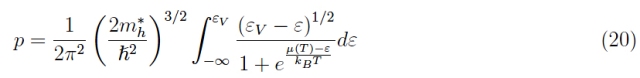
与金属不同，其中传导电子构成简并费米≪理想气体≫（因此，它表现出与玻尔兹曼统计量的偏差），半导体中的电子和空穴远未简并。从物理上讲，这意味着温度是这样的

因此，各个分布函数的指数分母就单位而言是主要的：

因此，方程 16 到 20 中的积分很容易计算，得到：

这可以看作是一个未知数μ （ T ） 中的两个方程组。对于任何半导体（内在或外在），我们都可以摆脱这个未知数，只需将两个方程相乘并使用指数，即可获得：

在哪里

是所讨论的半导体的带隙。请注意，此结果也适用于掺杂半导体。为了确定化学势，让我们参考n = p的本征半导体。根据公式 23：

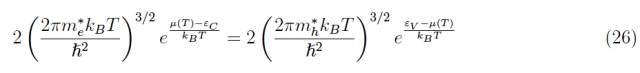
从中

如果m∗ h = m∗ e

也就是说，无论热力学平衡温度是多少，化学势都落在间隙的中间，如图 3 所示。

图 3：对于m∗ h = m∗ e，化学势落在间隙的中间。

再次考虑内在机制，它必须是n = p，因此等式 24 变为

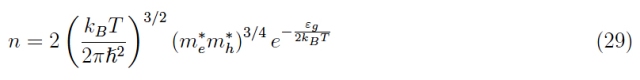
在等式 9 中替换返回：

取两边的对数：

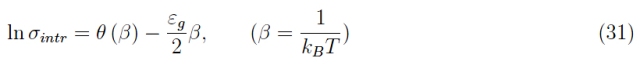
存在

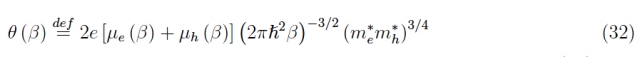
我们考虑了流动性对温度的依赖性。在比较等式 31 和等式 7 之前，让我们研究 （32） 对β → 0 +的行为。我们有：

因为在无限温度的限制下，我们期望无限的流动性。相反，在等式 7 中，我们在这里重写

常数 0 《 α 《 +∞ 是分布实验数据的直线原点的纵坐标。后者沿着指定的β min上升，低于该值的 ln σ intr 远离线性趋势，在 β → 0 + 即 T → +∞ 的极限内正向发散。但这只是理论上的趋势，因为对于T ≫ T 0我们预计半导体会被破坏。

将有效质量近似为电子质量 （ m ∗ ≃ m ∗ ≃ m e ）：

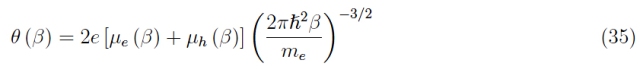
我们感兴趣的区间由公式 6 给出，并考虑迁移率常数

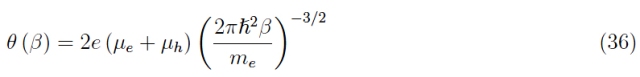
其中电子迁移率和间隙迁移率都在室温下冻结（方程式 10）。有了这个假设，公式 36 写成：

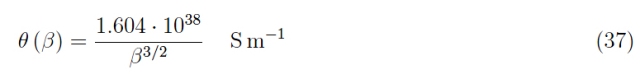
在上述区间中，它可以被认为是具有良好近似的常数（由于分子中的主导项）。所以让我们假设

我们现在可以写出插值线的方程：

考虑到实验数据σ intr （ β 0 ） = 2 。02 S/m，而使用MathemaTIca执行的拟合需要角线的系数，因此：

这是 SiC 半导体的典型带隙值。

审核编辑：郭婷