数模转换器(DAC)模型介绍

在本系列 ADC 建模的最后一部分中，我们将讨论另一个模型，并简要介绍 DAC 模型。

我们通过讨论建议的 ADC 仿真模型来结束我们的系列文章。

您可以通过以下链接了解对话：

如何为系统仿真建模数据转换器?

使用有效位数 (ENOB) 对 ADC 进行建模

使用互调多项式和有效位数对 ADC 进行建模

请记住，在本系列的第一篇文章中可以找到完整的缩写词列表、词汇表和完整的参考文献列表。

一个更好的 ADC 模型的建议

双音测试信号比单音提供更多关于 ADC 性能的信息。您作者的模型与特定 ADC 的制造商模型非常匹配，因此可以方便地运行误码率模拟。该 ADC 恰好具有非常宽的输入带宽。

对于带宽较低的 ADC，添加如图 1 所示的低通滤波器将提供更好的模型。

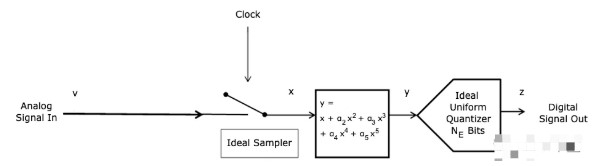
图 1. 基于上一篇文章的改进型 ADC 模型

此外，如我们上一篇文章的第一部分所述，改进的模型将允许添加高达 6 dB 的附加高斯白噪声，以更好地匹配真实 ADC 的本底噪声。

制造商的模型是“行为”模型，而不是精确模型。最好对详细的 SPICE 模型或实际物理设备上的测量进行相同的比较。

数模转换器 (DAC) 模型

参考文献 [19] 到 [26] 介绍了某种 DAC 模型，而 [27] 到 [29] 描述了 DAC 的特性，而不是模型。在这些展示模型中，大多数([19]、[20]、[22] 和 [23])展示了 DAC 设计人员而非用户似乎感兴趣的模型，提供了详细的特定模型来确定诸如 SNR 或输出频谱上的时钟抖动。

其他人提出的模型似乎太简单了。这些是[25]，它只考虑了没有量化的裁剪;和 [26]，将量化和裁剪建模为加性过程，仅对高斯输入有效。

参考文献 [21] 将 DAC 输出 (y(t)) 建模为 DAC 输入 (x(t)) 的函数，使用以下公式：

y(t) = x(t) + y HQ (x(t)) + y CM (x(t)) + y VQ (x(t))

等式 1

这些是相应的术语：

y HQ (x(t)) 考虑了“水平量化”(理想的时间采样)

y CM (x(t)) 说明“时钟源调制”(时钟抖动)

y VQ (x(t)) 考虑了“垂直量化”(幅度量化)，包括积分非线性。

这些项的表达式并不是非常复杂，因此这可能是模拟 DAC 的一个很好的模型。输入x(t)可以来自调制算法的浮点实现，或者来自具有输出 M 位的定点算法，其中 M > NE;其中 NE 是 DAC 的有效位数。

参考文献 [24] 提出了一个模型，该模型考虑了微分非线性 (DNL)、积分非线性 (INL)、增益和偏移误差、毛刺脉冲区域和稳定时间。

[24] 的图 5 显示了模型的框图。它由加性随机误差组成，用于对 DNL 进行建模;添加时间的确定性函数来模拟故障;用于对 INL、增益和偏移误差进行建模的多项式函数;延迟和时间转换(文中没有解释);一个低通滤波器来模拟建立时间;和噪声模型(文中也没有解释)。[24] 中的图 5 可以进行一些修改，在这里生成图 2，它是图 1 中 ADC 模型的逆;如果量化引起的输出噪声不够，则可以添加附加噪声。

图 2. 来自 Naoues, M. 的 DAC 模型的修改;莫什，D.;德霍斯，C.;巴拉克，R.;和 Ghazel, A, [24]

读者可能想知道为什么因为 DAC 的输入已经是数字的，所以还需要图 2 中的采样器和量化器。

通常，对于模拟，可以使用连续时间、浮点算法;将其转换为时钟定点版本是不值得的。(连续时间意味着模拟采样频率足够高，因此没有采样效应。)此外，DAC 接口上可用的实际位数(广告位数)通常大于 ENOB。