
作者丨弓青 来源丨古月居
如果说智能车的视觉处理是眼睛,PID就是双手可以去帮你完成智能车的运动控制。没有一个好的PID,就可能会产生手眼打架的情形。
比如说,你去看了一个美食博主的美食的制作过程,眼睛说,我会了,手说,你快拉到吧。
所以要想手眼协调,智能车控制得当,好的视觉处理算法和好的PID调试都密不可分。
不然也不会有专门的PID调试的岗位了。废话不多说,下面是我整理的一些资料。
方向控制在软件系统中的位置方向控制系统宏观概览
PID 控制方法理解
PID 程序编写PID 参数调试PID 算法微改进
方向控制算法在软件系统中的位置
整个智能车基本上就在做两件事,一个是方向的控制,一个是速度的控制(当然平衡车还多一个平衡的控制),只要能够将这两个量给控制的恰到好处(恰到好处不光是两者单独控制的很好,而是两者 一起工作时配合的很好)
本文档只讲其中的一个:方向控制中的控制策略问题(四轮车的速度控制与此非常类似,甚至还更简单)。
下面是我们车内软件运行的一个大概的流程图,软件成员后来的所有精力基本都倾注在这三个加粗的方面:方向偏差提取;方向控制算法;速度控制;
整体上就分为两部分,方向和速度控制。其中两者均为周期性控制,
但控制的周期可能不一样。方向控制的主要步骤如下:
1.采集方向传感器的信息,比如对于摄像头就是进行图像的采集;
2.方向偏差信息的求取,对于摄像头来说就是图像中线的求取, 进而得到得到车体当前位置与理想位置的偏差
3.方向控制模块根据这个偏差来计算应该输给舵机的PWM 占空比,进而来调整车体的前进方向。
方向控制系统宏观概览
系统宏观上了解。通过对系统的全局分析,你不仅可以更清楚了解方向控制的本质,更重要的是还能够从系统中各模块的相互约束关系中找到一些新的能够改进整个控制系统的方案,下面详述~
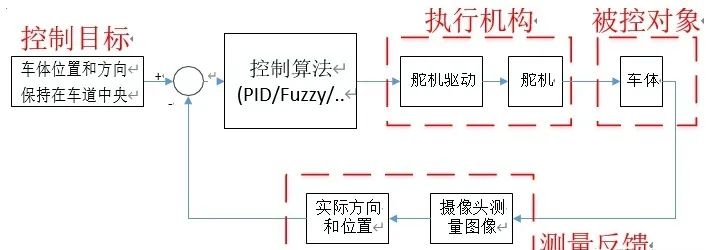
从控制系统的角度来看,典型的方向闭环反馈系统结构图如下图所示。
主要由五部分构成:控制目标;被控对象;执行机构;测量反馈;
控制算法(这里面就是我们常说的核心PID啦)
在构思控制算法之前你首先需要对执行机构,被控对象,测量反馈和控制目标
这四个部分有足够的了解。
控制目标是首当其冲要考虑的。本系统要控制的物理量是什么?
最开始想的肯定是保持车体的方向和位置在车道的正中央。
仔细思考一下可以发现,其实坚持的方向一直正确,最后的位置就一定会正确(感觉突然发现了一个在实际生活中也是颠扑不破的真理),而且车体的位置又是不可控(无能的舵机只能控制方向),因此其实控制目标可以换成只需要车体的方向保持正确就 OK了。
因此此时的系统变为如下。
要控制的物理量是车体前进方向:接下来要考虑执行机构与控制对象的特性。
本系统中的控制对象是什么?值得注意的是,本系统的执行机构是舵机驱动与舵机,被控对象是车体。
这一点重点关注执行机构与被控对象的输入-输出特性, 即输入 PWM 的占空比舵机转角的关系,舵机转角和车体转角的关系(为方便这里均近似看成是一个线性的比例关系,只是近似而已)
在接下来就该看测量反馈。
一个控制系统的精度的上限是由反馈测量部分精度决定,但是和这个上限的接近程度是由控制器来决定的。
控制策略再好,你测量的有误差也是白控制。因此才开始大家一定要注意将测量部分精度尽量提高,这样不仅能够大大减少控制部分的工作量,还能够有效提高控制精度。
个人感觉测量部分的重要性略大于控制部分。假设测量反馈的输入是摄像头图像,输出是方向信息,关键是怎么由图像得到方向信息?方向信息怎么表示?
按照我们目前方向角提取的方法(我们目前的做法:取图像中固定前瞻行(比如第 10 行)的中线的偏差来代替方向角。)
示意图如下图。
其中红色为车体,绿色为摄像头视野,蓝色为视野中求得的中线。
由图可以看出,其实这种方法其实是非常粗糙的。
那么如何得到更真实的方向信息,怎么改进?
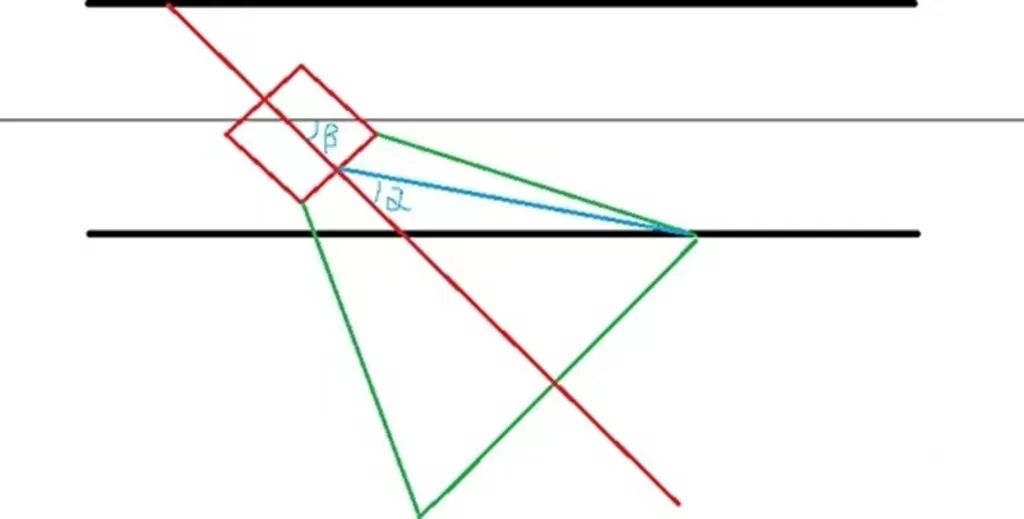
图像的中线能够反映出车辆的方向

图像的中线角度(alpha)近似反映出车辆的方向(beta)
关键问题:
从系统的角度来看我们可以采取怎么的方法来提升整体的控制精度?整个系统的关键部分在哪?如何改善关键部分的性能?
1) 执行机构与控制对象的改进。
舵机的机械传递结构改善、轮胎的摩擦力改善使控制的灵敏度更高,响应更快;使总体的输入输出能更接近线性比例关系(线性越好越容易控制)
2) 测量反馈的改善。
如何让测量的信息能够更真实的反映出车辆的方向信息。
对于摄像头和光电图像来说,就涉及到如何放置摄像头,如何取合适的图像视野,如何从对图像处理得到更有效的车辆真实方向信息(如先对图像进行失真矫正,然后对矫正以后的图像处理);
对于电磁传感器来说,那就是如何摆布各个电感的位置,如何使采集到的电压值更好的反应出方向信息(原始数据滤波融合等)等;
3) 控制策略的改善。
动态 PID,模糊控制,位置/增量PID,积分限幅,四轮车后轮双电机差速的协调控制等等
常用的控制策略-PID
PID 虽然是最简单的控制器,应用却是最广泛的,实际生活中 95%以上的控制都是 PID 控制。
还有很多其他控制方法,想法很好但是应用的实际效果却并不比 PID 好。
因此对于我们的小车控制来说,PID 完全足矣。
PID 的含义?(ProporTIon 比例+DifferenTIal 微分+Integral 积分)
输出量=P*误差+D*误差的变化+I*误差的积分
3.1 PID 的理解
l P(比例)控制,Kd 与Ki 为 0,最简单的控制规律
如直道(误差为 0)时舵机占空比 DUTY,则当误差为error 时,输出的占空比直接是 DUTY+Kp*error。
l PD(比例微分)控制,Ki 为 0
考虑偏差及偏差的变化趋势,当误差为 error 时,输出的占空比是 DUTY+Kp*error+Kd*(current_error-last_error)。可以看出,对于同样的一个偏差:
1) 若偏差正在减小的过程,PD 控制的量要比纯比例控制量小一些,这样能够避免过度控制
2) 若偏差在逐渐增加的过程,PD 所要施加的量比纯比例要多一些,目的是为了抑制误差增大的趋势。
所以 D 这一项有一些预测控制的味道~~~,相比 P 而言要更智能一些~~~
l PID(比例微分积分控制)
相比 PD 而言,多了一项积分项,目的是为了使系统无误差,将系统在整个过程中的误差考虑进去。当误差为error 时,输出占空比 DUTY+Kp*error+Kd*(current_error-
last_error)+Ki* error_integral
积分这一点对于方向控制来说意义不大,速度控制会需要。
不过有兴趣的均可以尝试一下。
3.2 PID 程序编写
//输出=P*误差+D*误差的变化+I*误差的积分int current_error,last_error ,error_integral; //偏差定义int Kp,Kd,Ki;//PID 参数定义int Out; //输出量current_error=get_error();//求出本次偏差 error_integral= error_integral+current_error; //误差积分 Out=Kp*error+Kd*(current_error-last_error)+Ki* error_integral; last_error=current_error;
注意:前面讲的 D 项都是对误差的偏差进行差 分,然而对于平衡车而言,官方方案里方向控制的 D 项被转向陀螺仪输出的角速度代替。
其作用也是起着一个预测的作用,且实际控制效果也非常好,因此四轮车也可以借鉴这种做法,在你们的车上装上一个陀~螺~仪~
3.3 参数调试(参照曲线) PID 的控制算法
非常简单,写起来总共也就 10 行不到,但我前面说了,你们后期的很大一部分时间还得花在这上面,这是为什么?
最耗时间的地方是什么?那就是参数的调试,也是你们在做车的后期 从不会间断的一件事。
理论上其实有很多参数调试方法,来快速得到一个合适的参数。
但是经过实践检验 的最实用的却还是—试凑,真是没办法,控制领域的科学家们努力了那么多年始终没能够找到一个特别行之有效的方法,只是因为工程实际与理论相差太远。
不过试凑也是要讲科学的,这也就是科学试凑法
(<( ̄ˇ ̄)>鄙人自己起的名字),试凑的依据就是下面同 P 不同 D 的曲线。其中横坐标为时间,纵坐标为输出(图中的 D 参数值只是示意大小关系,由此图可以大概得到某个参数应该调大还是调小),虚线为理想输出
记住曲线结论:----------------------- 非常重要
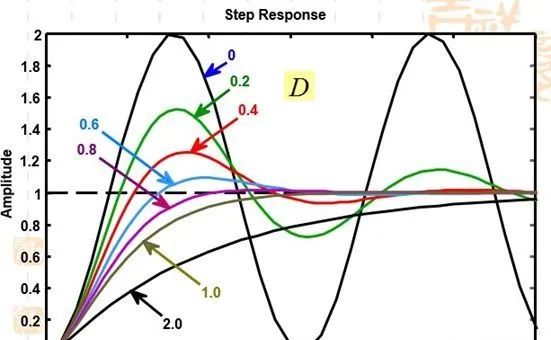
可以看出:
1) 对于同样的 P 而言,随着 D 的增加系统的超调量会越来越小,但是若 D 增加的太大会造成系统响应太慢,达不到控制要求。
2) 对于同样的 D 而言,P 增加过大会使系统震荡,超调大。对于方向控制而言,四轮车的 D 参数效果不太明显,但是平衡车的方向 D 参数调起来效果特别明显。
这个曲线的结论反映到你们实际的车上就是下面的行驶轨迹:
无 D 参数或 P 过大时,拐弯以后抖动比较厉害
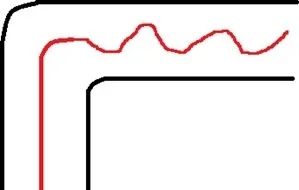
有 D 且 D 比较合适时,此时拐弯造成的抖动会明显减小
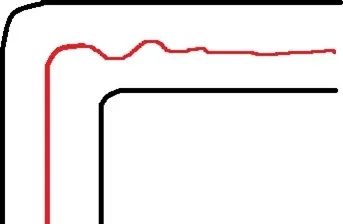
D 参数太大时,此时将会拐不过去
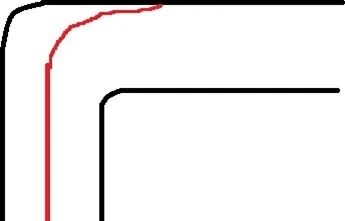
3.4 算法微改进
分段 PID/动态PID
PID 参数在运行的过程中根据时间的变化而变化。
如分段等,如考虑到当偏差较小时需要的控制量较小,而偏差较大时需要的控制量要增加,而这种增加客源是线性的,也可以是二次的,比如可以让 Kp 参数与偏差的平方成正比,如下图Kp = (error * error)/2 + 1000
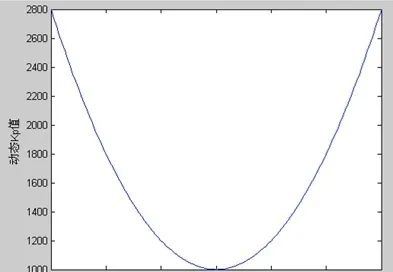
文章出处:【微信公众号:】欢迎添加关注!文章转载请注明出处。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)