伺服系统的惯量匹配原则

在伺服控制系统设计或是伺服电机的选型过程中，常常需要考虑惯量问题，惯量是影响伺服系统响应速度和稳定性的重要因素。总的来说，是希望系统的总体惯量越小越好，因为更小的系统惯量意味着更大的加速能力和更快的瞬态响应速度。在负载惯量一定的条件下，我们通常通过减小电机的转子惯量来达到降低系统总体惯量的目的，但这样的做法则不可避免的遇到惯量匹配的问题。

惯量匹配原则是指折算到电机轴的负载惯量与电机的转子惯量之比不能过大，必须小于一个推荐值，当惯量比过大时，系统一般会出现振荡甚至失控。这样一个原则被广泛接受和使用，但是很少有人去深究其内在的理论依据，伺服系统的设计者通常也并不十分清楚负载电机惯量比与系统稳定性的深层关系，因此惯量匹配原则始终作为一个经验法则存在着。

本文建立了一个简单的物理模型，用于分析惯量匹配对系统控制的影响，并基于此分析得到关于惯量匹配的实用性建议，为更好的理解负载电机惯量比与系统稳定性、响应性能等之间的关系，更合理的利用惯量匹配原则提供参考。

1.伺服系统建模

1.1 传统模型

在传统的伺服系统设计中，一般认为负载和电机之间的传动装置刚性是无穷大的，其模型示意图如图1：

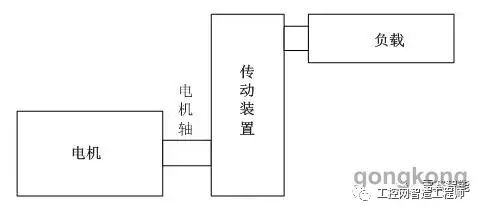
图1 简单的电机——负载传动模型

设定电机的转动惯量为JM;负载惯量为JL;传动比为i;传动效率为η;传动装置惯量为JC;电机轴转速为ωM;电机轴输出转矩为TM，系统满足以下基本方程：负载转速ωL：

负载转矩TL：

折算到电机轴的负载惯量JLM：

从以上表达式可以看出，如果使用减速比为i的减速器连接负载和电机，电机输出的转速将会下降为原来的1/ i;而折算到电机轴上的惯量会下降为原来的1/ i2，对于大惯量负载而言，这是降低负载电机惯量比的有效方法，但是系统的加速转矩也将会提高到原来的i倍。

如果系统满足惯量匹配，一般认为此时系统可以达到最大的能量传递效率，而负载也将获得最大的加速性能。为了确定负载电机惯量比与系统加速性能之间的关系，对图1中的系统作如下假定：

(1)直接耦合到电机轴上的齿轮或皮带轮的惯量作为电机转子惯量的一部分;

(2)直接耦合到负载轴上的齿轮或皮带轮的惯量作为负载惯量的一部分;

(3)忽略传动装置的效率、摩擦和自身惯量等因素;系统满足方程：

(1) 电机的加速度为：

(2) 其中为

负载的加速度。

由(1)、(2)两式可以推出，负载的加速度为：

(3) 电机的输出转矩TM一定，要知道最大负载加速度时的惯量比，即需要知道确定最大负载加速度时对应的传动比i的值，式(3)对i求导，得：

(4) 令式(4)等于0;得：

(5)

由式(5)不难算出，当负载获得最大加速度时，折算到电机轴的负载惯量JLM与电机转矩JM之比为1:1。从以上分析可知，在理想状态下，调整负载电机惯量比为1:1有助于系统的加速性能。但在实际应用过程中，由于传动装置的效率，空程间隙等机械特性，传动装置自身的惯性，负载的反冲作用，系统的传动刚性等诸多因素的影响，设置负载惯量比为1:1并不具有很高的效率，而且增加减速比的方式也会提高整个系统所需要的加速转矩。

在如上诸多因素中，系统的传动刚性是最需要考虑的问题，因为在系统传动刚性较差的前提下，如果负载电机的惯量比过大将会导致系统振荡，出于系统稳定性的考虑，需要修改电机到负载的传动模型。

1.2改进模型

使用一根d性轴作为连接负载和电机的传动装置，忽略传动装置的内部细节，忽略d性轴直径等次要因素，仅仅将注意力放在传动刚性上，基于以上假设建立负载和电机之间的传动模型，其示意图如图2：

图2 电机——负载d性传动模型

图中：TM为电机的输出转矩;TL为负载转矩;BM和BL分别为电机和负载的粘性摩擦系数;KS为d性轴的抗扭刚度;ωM和ωL分别是电机和负载的转速，θM和θL分别表示电机和负载角位移，θS为d性轴的扭转度。

JM和JL分别为电机和负载的转动惯量，系统满足运动方程：

(6)

(7)

(8) 使用式(6)、(7)、(8)可以得到电机和负载速度响应，通过拉氏转换求得其传递函数，分别表示为：

(9)

(10) 其中式(9)为电机的速度响应、式(10)为负载的速度响应。

θS是一个与表征系统振荡特性的变量，忽略粘性摩擦系数，由式子(8)、(9)、(10)可得：

(11) 使用一个单位阶跃力矩TS作用于系统，对式(11)做拉氏转换的逆运算可得：

(12) 其中Ir为负载电机惯量比，即：

式(12)为表征系统的振荡特性的表达式。从式(12)可以看出，增大系统的传动刚度将升高振荡的频率，但会降低振荡的幅值，当系统的传动刚度为无穷大时，振荡消失。小范围内增大惯量比将小幅度的降低振荡频率，同时小幅度增大振荡幅值，但是当惯量比很大的时候，较小范围调整惯量比的值对系统振荡已经没有明显的影响。总而言之，相比较惯量比而言，系统的传动刚性是影响系统稳定性的更重要的因素。

2. 惯量匹配的实用性原则

如果系统传动刚性为无穷大，那么负载电机惯量比也可以设置到无穷大。对于一个无限传动刚性的系统而言，负载惯量和电机惯量可以看做统一的整体，甚至可以认为负载和电机轴是一体的，此时惯量比不再成为问题，惯量匹配原则也将失效。从上文的分析可知，负载电机惯量比并不是导致系统振荡的主因，而只是振荡的指示标志，其更大的原因是系统的传递刚性，如何希望根除系统振荡现象，更多的时候应该从增大系统传动刚性的角度下功夫。

对于通常条件下使用到的传动装置，我们也可以通过式(12)来做定性分析，从式中我们可以知道对于小范围内变化的负载惯量，可以通过增大系统传动刚性Ks、或是降低负载电机惯量比来规避系统振荡，但是对于确定负载电机惯量比的上限，通常的办法是利用经验法则。

对于常见的滚珠丝杠伺服系统，一般认为当惯量比大于10:1时系统对负载惯量的变化将变得十分敏感，而对于步进电机的控制，一般认为惯量比大于2:1~3:1时，系统将变得难以控制，实际上摩擦对降低振荡是有帮助的，步进电机的定位转矩对吸收振荡有一定的作用，通常情况下步进电机的惯量比上限可达到4:1~5:1。另外对于有些伺服电机宣称的可以达到惯量比50:1，实际上是保持系统稳定性条件下明显牺牲系统的加速性能的一种控制方式，并不在本文的讨论范围内。

3. 结论

本文讨论的d性轴负载——电机传动模型，可以清晰直观的帮助了解系统稳定性与负载电机惯量比之间关系。但由于此模型中未提及传动装置内部摩擦、负载的反冲作用力等诸多影响伺服系统稳定性的因素，在实际应用中仍有其局限性。

审核编辑：汤梓红