如图,在RT△ABC中,∠C=90°,AC=3根号3 ,BC=9,点Q是边AC上的动点（点Q不与点A、C重合）

1、∵QR∥AB，∴∠B=∠QRC，∵△QCR沿QR翻折后得到△QPR，∴∠QRC=∠PRQ

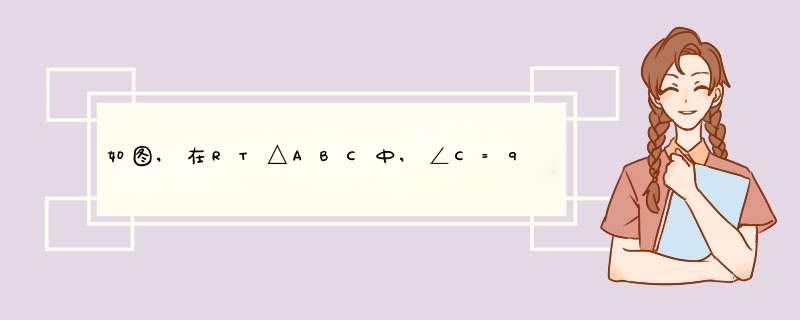
∴∠PRQ=∠B，∵AC=3√3，BC=9，∠ACB=90°，∴tan∠B=√3/3，既∠B=30°

∴∠PRQ=30°

2、∵∠QPR=∠ACB=90°（翻折关系），∠PRQ=30°，∠PQR=180°-∠QPR-∠PRQ

∴∠PQR=∠CQR=60°（翻折关系），∴∠AQP=180°-∠PQR-∠CQR=60°

∵∠A=180°-∠ACB-∠B=60°，∴△APQ为等边三角形（两个内角为60°的三角形）

∴AQ=PQ，∵PQ=CQ（翻折关系），∴AQ=CQ=1/2AC=3√3/2，既x=3√3/2

3、应该是PE=y吧？前面没提到过D啊

设PQ与AB交点为F

同理可证∠PQR=∠AQP=60°（和第二问证法完全一样），∴△AQF为等边三角形

∴AQ=QF=x，∵QC=AC-AQ，∴QC=3√3-x，∵tan∠QRC=√3/3

∴QC/CR=√3/3，∴CR=√3(3√3-x)，∵PF=PQ-QF，∴PF=3√3-2x

∵PR=CR（翻折关系），∴PR=√3(3√3-x)，∵PQ=CQ（翻折关系），∴PQ=3√3-x

∵QR∥AB，∴△PEF∽△PQR，∴PF/PQ=PE/PR

∴(3√3-2x)/(3√3-x)=y/√3(3√3-x)，

化简后得：y=9-2√3x

∵Q在AC上移动，且不与A、C重合，∴3√3>x>0

电影《爆炸新闻》的豆瓣评分是7.2。

该片改编自真实事件，福斯新闻台高管罗杰在2016年被曝光了性骚扰丑闻，女主播梅根和格雷琴都遭遇了对方的骚扰，这起事件在媒体界引发轩然大波的故事。

链接: https://pan.baidu.com/s/19vE0S5SnlRFfl2DvHqcqrA

?pwd=u1yt 提取码: u1yt

《爆炸新闻》展示了主播们光鲜亮丽的外表背后不为人知的辛酸。查理兹·塞隆捕捉到了梅根独特而自信的说话方式和措辞。她的表演展现出了梅根这个角色的复杂性和矛盾性使得角色非常人性化。她刻意凸显了梅根高冷的气质，模仿了她铿锵有力的口音。这种改变令人印象深刻，这是其职业生涯里精彩的表现之一。

该片对于职场环境正逐渐变得多样化的其他国家来说，片中的故事情节也能引发共鸣。作为一个独立的故事，影片非常精彩地呈现了滥用权力者最终自食恶果的过程，在事件还原上做到了很大程度的忠实。

---