什么是Box-Cox?

Box-Cox 转换的基本假设是:

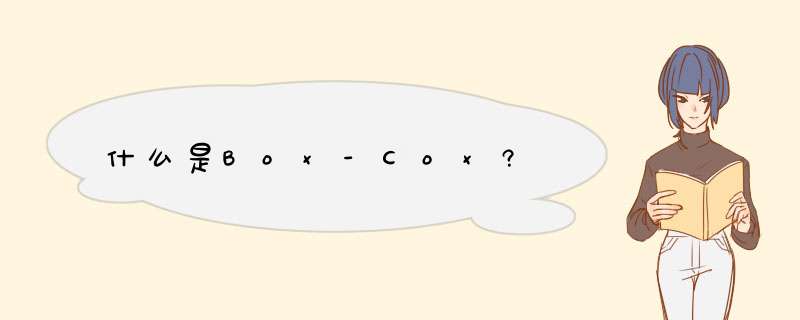
反应变数 (资料) 做一乘幂变换后, 符合常态分布。

在这假设之下, 产生下列结果:

(1) 由于要决定的是「乘幂」部分, 也就是我们要考

虑指数函数 Y ->Y^r (在此 r 是要被选择的,

因此是「变数」)

但此函数当 r=0 时恒为 1。因此, 若直接考虑此

形式, 将造成必须把 0 排除的问题。为解决此问

题, 将原转换做修改, 成为

Y ->(Y^r-1)/r

当 r<>0 时, 这只是原转换做平移及尺度调整, 但

当 r->0 时, 却可得一极限式

(Y^r-1)/r ->ln(Y)

因此, r=0 时, 乘幂变换定义为 ln(Y), 是「系统

化」必然的结果。

(2) 将 $r$ 当成一个参数, 假设 (Y^r-1)/r 服从常态

分布, 形成常态模型的一个扩充模型。于是我们可

以用适当的方法去估计 r。目前常用的是 MLE, 在

BMDP 中有一程序可自动计算 r 的 MLE (但是哪个

程序我不清楚)。不过, 也有学者认为, r 不应是

任意值, 因为那样在模型解释上不方便 (谁能解释

说销售量和售价的关系是 Y^0.0245=a-bx﹖) 因此,

实务上可以:

a) 以软体计算出 r 的 MLE 后再取一靠近 MLE 但

较易了解和解释的 r 值。

b) 以便于解释的一些可能 r 值一一代入计算, 选

一个在某一准则上最适当 (如 likelihood 最高)

的 r 值。

MLE 是在「常态性」假设下的做法。在此假设下, 我们

还可对 r 做推论, 如下午路老师谈到的: 检定转换的必

要性 (或两种转换之间的选择), 或做 r 的区间估计。

后者在不直接用 r 的 MLE 而用「大略值」时尤其重要。

日前路老师提到一个问题: 假设不成立时呢﹖

乘幂的 MLE 是在常态性假设之下推导而得的。但有时我

们由散布图直观地认为可对反应变数做一适当转换, 使

某一特定形式的曲线较适合转换后资料。这是和前述 MLE

完全不同的想法----不是要改善常态性而可能是要改善

直线性。这样的想法也未尝不可, 只是仅限于从乘幂变换

去寻求「适当」变换式, 未免太狭隘。不过, 当然对此批

评, 我们也可辩解, 例如: 在「改善常态性」这观点, 可

考虑的变换也不只是乘幂变换啊! 然而, 另一方面, 以改

善直线性为着眼, 如何对 r 做推论, 却是个问题。SSE 是

一直观、叙述性指标, 不知有无讨论利用它做推论的文献﹖

(若没有, 似可当做硕论的题目。)

再者, 上述 SSE 应以原尺度计算较合理。

是否一条formula?

是一条formula。

有什么用途?

通过BOX-COX数据转换分析，确定热氧化工艺目标值的最优转换形式，针对转换后数据建立的回归模型满足上述假设。结果表明：数据转换的建模方法能满足方差分析的假设（违反度减轻），并且能更多发掘数据信息，氧化膜厚的模型拟合修正判定系数R^2由93.54%增加到98.64%。所得模型用于优化工艺条件，在满足膜厚目标下，非均匀性由0.2%减小到0.08%。文中讨论的基于数据转换的建模方法可以用于半导体制造其他工艺。,

这个课题太大!因为涉及半导体材料的泛范围太广了!简单地说:以半导体材料及衍生材料为主体的各种工艺研发和制造都称为半导体工艺!半导体:顾名思义!就是导电率介于导体和绝缘体之间的金属及非金属材料!常见的硅,锗,都属于此类!

半导体的范围广泛，应用从科研到民生，日新月异:

1.制造工艺需根据半导体设计的层层不同而不同，2.为避免复杂繁琐导致质量问题，制造工艺流程基本上分三个工程段落，

2.1.模组及应用设计工程，模拟数据

2.2.前工程

2.3.后工程封测

每个阶段都有上百到三百种以上的工艺，至少需要学习10-30年

---