根号(x+1x)不定积分

不能表示为初等函数根据切比雪夫定理可以判断

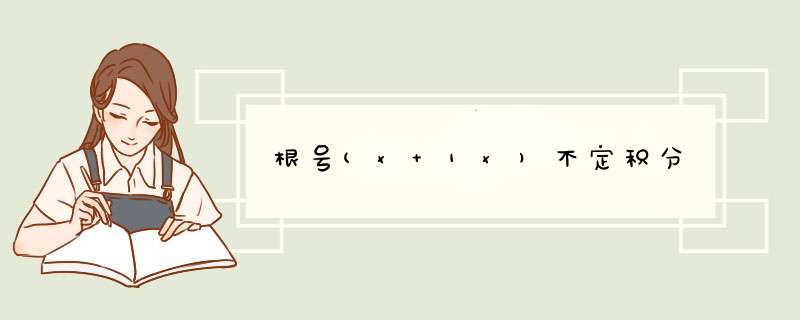
切比雪夫定理：二项微分式∫x^p(1+x^r)^qdx （其中a,b不等于0,p,q,r均为有理数）能表示为初等函数的充分必要条件为q、（p+1)/r、（p+1)/r+q中至少有一个为整数

答案如图所示：

一次积分完的话，那个函数不是初等的

：

如果一个函数的积分存在，并且有限，就说这个函数是可积的。一般来说，被积函数不一定只有一个变量，积分域也可以是不同维度的空间，甚至是没有直观几何意义的抽象空间。如同上面介绍的，对于只有一个变量x的实值函数f，f在闭区间[a,b]上的积分记作

其中的  除了表示x是f中要进行积分的那个变量（积分变量）之外，还可以表示不同的含义。在黎曼积分中，  表示分割区间的标记；在勒贝格积分中，表示一个测度；或仅仅表示一个独立的量（微分形式）。一般的区间或者积分范围J，J上的积分可以记作

如果变量不只一个，比如说在二重积分中，函数  在区域D上的积分记作

 或者  其中  与区域D对应，是相应积分域中的微分元。

参考资料：