已知Ackerman函数定义如下：

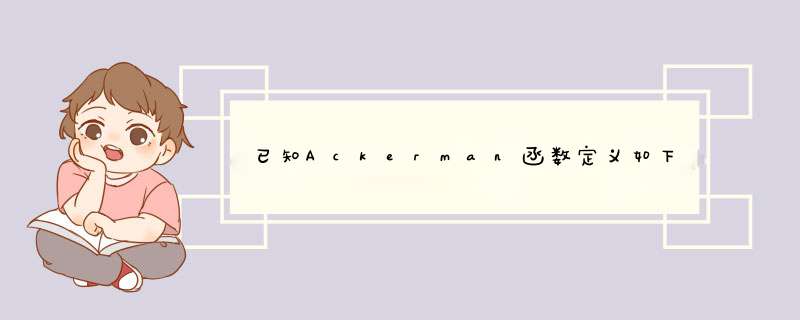
//（1）递归算法如下： 

int akm(int m,int n)

{//递归设计

 int r,g;  

 if(m==0) r=n+1; 

 else if(n==0) r=akm(m-1,1);  

 else { 

 g=akm(m,n-1);r=akm(m-1,g);//两次连着递归  }  

 return r;  }

 //（2）利用栈

 void main()

  { 

   int m=3;int n=2; 

   struct {

   int mval;

   int nval;

   int ack;}s[100]; 

   int top=0;

 s[top]mval=m;

 s[top]nval=n;

 s[top]ack=-1;

 while(s[0]ack==-1)

  { 

    if(s[top]mval==0)

     { s[top]ack=s[top]nval+1; 

       while(s[top]ack!=-1&&top)

       {

        top--;

        if(s[top]nval==-1){ s[top]nval=s[top+1]ack;} 

        else { s[top]ack=s[top+1]ack;} 

        } 

         } 

     else if(s[top]nval==0) 

            { 

            top++;

            s[top]mval=s[top-1]mval-1; 

            s[top]nval=1;

            s[top]ack=-1;

                  }

            else 

                 {

                  top++;

                  s[top]mval=s[top-1]mval-1; 

                  s[top]nval=-1; 

                  s[top]ack=-1;

                  top++;

                  s[top]mval=s[top-2]mval;

                  s[top]nval=s[top-2]nval-1;

                  s[top]ack=-1;

                  }

                     } 

 cout<<s[0]ack<<endl;}

在程序编辑过程中，我们可能会遇到这样一类问题，出题者告诉你数列的前几个数，或通过计算机获取了数列的前几个数，要求编程者求出第N项数或所有的数列元素（如果可以枚举的话），或求前N项元素之和。这种从已知数据入手，寻找规则，推导出后面的数的算法，称这递推算法。

在处理递推问题时，我们有时遇到的递推关系是十分明显的，简单地写出递推关系式，就可以逐项递推，即由第i项推出第i+1项，我们称其为显示递推关系。但有的递推关系，要经过仔细观察，甚至要借助一些技巧，才能看出它们之间的关系，我们称其为隐式的递推关系。

递推算法的关键是认真分析题意，发现递推关系，正确写出递推公式，求得边界条件，然后用循环实现即可。

总结

1递推算法的基本形式，是指编程者让计算机循环求得一序列数值，而后一项的计算结果是由上一项或多项推导出来的。有时，我们为求得一个数列的某一项，我们不得不从第一项开始，逐个计算前面每一项的值。虽然这样做的效率不很高，但它能帮助我们解决许多实际问题。

2无论是顺着还是逆着递推，其关键是递推公式是否正确，边界条件是否正确。二者有一个出错。则所有递推结果将都是错误的。

例1：已知数列1，2，5，10，17，26，37求数列的第n项。

通过分析，我们可以发现，数列后面的数在前一项的基础上以1，3，5，7，9，11的规律增长，则可以得出增长规律的表达式为2n-3,也就是a(1)=1,a(n)=a(n-1)+2n-3;

还有一个规律，我们可以发现每一项依次为从0开始的自然数的平方再加1，即

(n-1)2+1,第一项（1-1）2+1，第二项（2-1）2+1，第三项（3-1）2+1

例2:阶梯问题：题目的意思是：有N级阶梯，可以一步走上一级，也可以一步走两级，求从阶梯底走到顶端可以有多少种不同的走法。

这是一个隐式的递推关系，如果编程者不能找出这个递推关系，可能就无法做出这题来。我们来分析一下：走上第一级的方法只有一种，走上第二级的方法却有两种（两次走一级或一次走两级），走上第三级的走法，应该是走上第一级的方法和走上第二级的走法之和（因从第一级和第二级，都可以经一步走至第三级,也就是说增加的第三级有两种处理方法，第一种就是直接作为一级走一步，那么就和两级的走法一致，另一种就是与第二级合并作一步走，那么就和一级的走法一致，加起来就是一级的方法和二级的走法之和），推广到走上第i级，是走上第i-1级的走法与走上第i-2级的走法之和。很明显，这是一个菲波拉契数列。到这里，读者应能很熟练地写出这个程序。在以后的程序习题中，我们可能还会遇到菲波拉契数列变形以后的结果：如f(i)=f(i-1)+2f(i-2)，或f(i)=f(i-1)+f(i-2)+f(i-3)等。

例3：猴子吃桃问题：山中住有五只猴。一天，老大看见一堆桃子，想把桃子据为已有，却担心让老二老三知道了说自己太贪心。于是将桃分成相等的两份，却发现剩余一个，于是，老大吃掉这一个以后，再带走这堆桃的二分之一。第二天，老二也看到了这堆桃，其想法和做法与老大一样，老三老四老五也和他们的兄长想到一块去了。结果等老五吃完一个，带走一半以后，这堆桃还剩余11个。请编程计算当初这堆桃共有多少个。

这个下题目明眼人一看便知，我们如果按兄弟吃桃把桃的相反顺序倒推过去，就能知道当初桃子的总数。其递推的公式是a[n-1]=a[n]2+1。递推的初始值是a[5]=11（又称边界条件），待求a[0]的值。相信现在大家能很容易就能写出正确的程序。在这里不过是想说明一下，递推算法不仅可以顺着推、也可逆着推的道理。

回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。

用回溯算法解决问题的一般步骤为：

　　一、定义一个解空间，它包含问题的解。

　　二、利用适于搜索的方法组织解空间。

　　三、利用深度优先法搜索解空间。

　　四、利用限界函数避免移动到不可能产生解的子空间。

问题的解空间通常是在搜索问题的解的过程中动态产生的，这是回溯算法的一个重要特性。

　　回溯法是一个既带有系统性又带有跳跃性的的搜索算法。它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解。如果肯定不包含，则跳过对以该结点为根的子树的系统搜索，逐层向其祖先结点回溯。否则，进入该子树，继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。而回溯法在用来求问题的任一解时，只要搜索到问题的一个解就可以结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法，它适用于解一些组合数较大的问题

[递推是学习材料，回溯是]

江静

游客 回答于：2010-8-29 15:05:18

递归

递归是计算机科学的一个重要概念,递归的方法是程序设计中有效的方法,采用递归编写

程序能是程序变得简洁和清晰

21 递归的概念

1概念

一个过程(或函数)直接或间接调用自己本身,这种过程(或函数)叫递归过程(或函数)

如:

procedure a;

begin

a;

end;

这种方式是直接调用

又如:

procedure b; procedure c;

begin begin

c; b;

end; end;

这种方式是间接调用

例1计算n!可用递归公式如下:

1 当 n=0 时

fac(n)={nfac(n-1) 当n>0时

可编写程序如下:

program fac2;

var

n:integer;

function fac(n:integer):real;

begin

if n=0 then fac:=1 else fac:=nfac(n-1)

end;

begin

write('n=');readln(n);

writeln('fac(',n,')=',fac(n):6:0);

end

例2 楼梯有n阶台阶,上楼可以一步上1阶,也可以一步上2阶,编一程序计算共有多少种不同的走法

设n阶台阶的走法数为f(n)

显然有

1 n=1

f(n)={2 n=2

f(n-1)+f(n-2) n>2

可编程序如下：

program louti;

var n:integer;

function f(x:integer):integer;

begin

if x=1 then f:=1 else

if x=2 then f:=2 else f:=f(x-1)+f(x-2);

end;

begin

write('n=');read(n);

writeln('f(',n,')=',f(n))

end

22 如何设计递归算法

1确定递归公式

2确定边界(终了)条件

练习:

用递归的方法完成下列问题

1求数组中的最大数

21+2+3++n

3求n个整数的积

4求n个整数的平均值

5求n个自然数的最大公约数与最小公倍数

6有一对雌雄兔,每两个月就繁殖雌雄各一对兔子问n个月后共有多少对兔子7已知:数列1,1,2,4,7,13,24,44,求数列的第 n项

23典型例题

例3 梵塔问题

如图:已知有三根针分别用1,2,3表示,在一号针中从小放n个盘子,现要求把所有的盘子

从1针全部移到3针,移动规则是:使用2针作为过度针,每次只移动一块盘子,且每根针上

不能出现大盘压小盘找出移动次数最小的方案

程序如下:

program fanta;

var

n:integer;

procedure move(n,a,b,c:integer);

begin

if n=1 then writeln(a,'--->',c)

else begin

move(n-1,a,c,b);

writeln(a,'--->',c);

move(n-1,b,a,c);

end;

end;

begin

write('Enter n=');

read(n);

move(n,1,2,3);

end

例4 快速排序

快速排序的思想是:先从数据序列中选一个元素,并将序列中所有比该元素小的元素都放到它的右边或左边,再对左右两边分别用同样的方法处之直到每一个待处理的序列的长度为1, 处理结束

程序如下:

program kspv;

const n=7;

type

arr=array[1n] of integer;

var

a:arr;

i:integer;

procedure quicksort(var b:arr; s,t:integer);

var i,j,x,t1:integer;

begin

i:=s;j:=t;x:=b[i];

repeat

while (b[j]>=x) and (j>i) do j:=j-1;

if j>i then begin t1:=b[i]; b[i]:=b[j];b[j]:=t1;end;

while (b[i]<=x) and (i<j) do i:=i+1;

if i<j then begin t1:=b[j];b[j]:=b[i];b[i]:=t1; end

until i=j;

b[i]:=x;

i:=i+1;j:=j-1;

if s<j then quicksort(b,s,j);

if i<t then quicksort(b,i,t);

end;

begin

write('input data:');

for i:=1 to n do read(a[i]);

writeln;

quicksort(a,1,n);

write('output data:');

for i:=1 to n do write(a[i]:6);

writeln;

end

练习:

1计算ackerman函数值:

n+1 m=0

ack(m,n)={ ack(m-1,1) m<>0 ,n=0

ack(m-1,ack(m,n-1)) m<>0,n<>0

求ack(5,4)

　回溯

回溯是按照某种条件往前试探搜索,若前进中遭到失败,则回过头来另择通路继续搜索

31 回溯的设计

1用栈保存好前进中的某些状态

2制定好约束条件

例1由键盘上输入任意n个符号;输出它的全排列

program hh;

const n=4;

var i,k:integer;

x:array[1n] of integer;

st:string[n];

t:string[n];

procedure input;

var i:integer;

begin

write('Enter string=');readln(st);

t:=st;

end;

function place(k:integer):boolean;

var i:integer;

begin

place:=true;

for i:=1 to k-1 do

if x[i]=x[k] then

begin place:=false; break end ;

end;

procedure print;

var i:integer;

begin

for i:=1 to n do write(t[x[i]]);

writeln;

end;

begin

input;

k:=1;x[k]:=0;

while k>0 do

begin

x[k]:=x[k]+1;

while (x[k]<=n) and (not place(k)) do x[k]:=x[k]+1;

if x[k]>n then k:=k-1

else if k=n then print

else begin k:=k+1;x[k]:=0 end

end ;

end

例2n个皇后问题:

program hh;

const n=8;

var i,j,k:integer;

x:array[1n] of integer;

function place(k:integer):boolean;

var i:integer;

begin

place:=true;

for i:=1 to k-1 do

if (x[i]=x[k]) or (abs(x[i]-x[k])=abs(i-k)) then

place:=false ;

end;

procedure print;

var i:integer;

begin

for i:=1 to n do write(x[i]:4);

writeln;

end;

begin

k:=1;x[k]:=0;

while k>0 do

begin

x[k]:=x[k]+1;

while (x[k]<=n) and (not place(k)) do x[k]:=x[k]+1;

if x[k]>n then k:=k-1

else if k=n then print

else begin k:=k+1;x[k]:=0 end

end ;

end

回溯算法的公式如下:

32 回溯算法的递归实现

由于回溯算法用一栈数组实现的,用到栈一般可用递归实现。

上述例1的递归方法实现如下：

program hh;

const n=4;

var i,k:integer;

x:array[1n] of integer;

st:string[n];

t:string[n];

procedure input;

var i:integer;

begin

write('Enter string=');readln(st);

t:=st;

end;

function place(k:integer):boolean;

var i:integer;

begin

place:=true;

for i:=1 to k-1 do

if x[i]=x[k] then

begin place:=false; break end ;

end;

procedure print;

var i:integer;

begin

for i:=1 to n do write(t[x[i]]);

writeln;readln;

end;

procedure try(k:integer);

var i :integer;

begin

if k=n+1 then begin print;exit end;

for i:=1 to n do

begin

x[k]:=i;

if place(k) then try(k+1)

end

end;

begin

input;

try(1);

end

例2：n皇后问题的递归算法如下：

程序1：

program hh;

const n=8;

var i,j,k:integer;

x:array[1n] of integer;

function place(k:integer):boolean;

var i:integer;

begin

place:=true;

for i:=1 to k-1 do

if (x[i]=x[k]) or (abs(x[i]-x[k])=abs(i-k)) then

place:=false ;

end;

procedure print;

var i:integer;

begin

for i:=1 to n do write(x[i]:4);

writeln;

end;

procedure try(k:integer);

var i:integer;

begin

if k=n+1 then begin print; exit end;

for i:= 1 to n do

begin

x[k]:=i;

if place(k) then try(k+1);

end;

end ;

begin

try(1);

end

程序2：

说明:当n=8 时有30条对角线分别用了l和r数组控制，

用c数组控制列当(i,j)点放好皇后后相应的对角线和列都为false递归程序如下:

program nhh;

const n=8;

var s,i:integer;

a:array[1n] of byte;

c:array[1n] of boolean;

l:array[1-nn-1] of boolean;

r:array[22n] of boolean;

procedure output;

var i:integer;

begin

for i:=1 to n do write(a[i]:4);

inc(s);writeln(' total=',s);

end;

procedure try(i:integer);

var j:integer;

begin

for j:=1 to n do

begin

if c[j] and l[i-j] and r[i+j] then

begin

a[i]:=j;c[j]:=false;l[i-j]:=false; r[i+j]:=false;

if i<n then try(i+1) else output;

c[j]:=true;l[i-j]:=true;r[i+j]:=true;

end;

end;

end;

begin

for i:=1 to n do c[i]:=true;

for i:=1-n to n-1 do l[i]:=true;

for i:=2 to 2n do r[i]:=true;

s:=0;try(1);

writeln;

end

练习：

1找出所有从m个元素中选取n(n<=m)元素的组合。

2设有A,B,C,D,E 5人从事j1,j2,j3,j4,j5 5项工作每人只能从事一项,它们的

效益表如下:

　j1j2j3j4j5A13111047B13101085C59774D151210115E1011884

求最佳安排,使效益最高

3N个数中找出M个数(从键盘上输入正整数N,M后再输入N个正数),要求从N个数中

找出若干个数,使它们的和为M,把满足条件的数组找出来,并统计组数

4地图着色。如下图12个区域用4种颜色着色要求相邻的区域着不同的颜色

5将任意一正整数(1<n<100)分解成若干正整数的和

如:4=1+1+1+1

=2+1+1

=2+2

=3+1

直接在ADAMS/CAR里建模，建完模里边有软件自带的几种仿真，比如双轮同向，反向激振，转向仿真，整车仿真等，运行完进入postprosessor界面，里面有很多软件自带的函数测量，选择要绘图的参数绘图就能绘制仿真过程中各个参数的变化，里面有ackerman这一项的，ADAMS/CAR很好用的，汽车建模比VIEW真实多了，就是需要添加一些通讯器，安装件，这些添加不好仿真就容易不成功

1 计算Y值:

COS(X+30) 0≤X<10

Y= (COS(X+75))2 10≤X<20

(COS(X+40))4 20≤X<30

2 读入一个三位数字的正整数,将其反向输出

3 输出三个数中的最大数

4 x,y,z的值分别为1,11,111,将它们靠左边对齐输出

5 x,y,z的值分别为1,11,111,将它们靠右边对齐打印输出

6 对于输入的方程系数,求二元一次方程组的解

7 输入两整数,求出它们的最大公约数和最小公倍数

8 对于输入的MAX个数字,统计其中奇,偶数的个数

9 找出10个数中的最大和最小数字

10 吉普车问题希望一辆吉普车以最少的燃料消耗跨越1000公里的沙漠 现已知吉普车总装油量为500升,耗油率为 1 升/公里在沿途无加油站 所以利用吉普车自己运油逐步前进问要多少油才能使吉普车以最少油耗跨越 1000公里沙漠

11 求下面第N个fibonacci数其定义为

f(0)=0,f(1)=1,f(n)=f(n-1)+f(n-2) (n>=2)

12 求下面的Armstrong数,Armstrong数是一个N位数,它的值等于每位数字的N次幂的和例如153=1^3+5^3+3^3试求999以内的Armstrong数

13 马戏团有鸟和大象,它们共有 36 个头,100只脚问有多少只鸟和大象

14 100匹马驮100担货,大马一匹驮3担,中马一匹驮2担,小马2匹驮1担计算大,中,小马的数目

15 打印数字金字塔

1

1 2 1

1 2 3 2 1

1 2 3 4 3 2 1

16 找出2000以内的勾股数 (a2=b2+C2)

17 将1元钱兑换成1,2,5分及1,2,5角钱,有多少种可能

18 打印乘法口诀表

19 有一对兔子,出生一个月后变成一对小兔子,两个月后生出第一小兔子, 自己变成一对老兔子,此时共有二对兔子,(一老一小),三个月后,老兔子又生出一对小兔子,上个月生的小兔子变成大兔子,此时共有三对(老,大小各一对),四个月后,大变老,小变大,二对老兔子又生二对小兔子,此时共有五对(老,小各二对,大的一对)计算11个月后共有多少对兔子？

20 打印方阵

A B C D E

B C D E A

C D E A B

D E A B C

E A B C D

21 按字母表顺序和逆序每隔一个字母打印即输出如下:

a c e g i k m o q s u w y

z x v t r p n l j h f d b

22 计算机产生一个 0-100的随机整数,由你猜计算机对你猜的数分别不同情况作出三种不同的反应,太大(TOO BIG),太小(TOO SMALL),正好(FIT)当猜着时,就输出你猜的次数和猜中的数

23 如果一个自然数等于它的全部约数(不包括这个数本身)之和,则这个自然数称为完全数例如6本身以外的约数为 1,2,3,而6=1+2+3所以6是一个完全数求出自然数中前3个完全数

24 将一真分数写成几个分子是一的分数的和的形式

25 有趣的数学问题: 某学校组织 M 名学生前往离校 X 公里处参加军事训练可是,目前只有一部可坐 N 个人的汽车,其中M>=N假如已知学生们的步行速度为A公里/小时,汽车的速度是 B 公里/小时,其中 A<B,学生们上下车的时间忽略不计,试设计一个程序求出全体学生到达目的地的最短时间

26 现有零件若干盒,每盒有零件100个,一个小组在制作某种机器时,需要这种零件,第一,二天不需要,第三天需要3个,第四天需要4个,第N天需要N天需要N个,已知此小组工作了40天以上,且恰好用了M盒零件,5<=M<=10,问此小组一共工作多少天,用了几盒零件

27 验证哥德巴赫猜想任意大于 6 的偶数均可表示为二素数之和

28 编程找出M,N(M<N,N为自然数)为何值时,1989的M次方与1989的N次方的最后三位数相等,且M+N的值最小

29 求1/a+1/b,1/a+1/b+1/c,a/b+c/d的最简分数值

30 打印

1 2 3 4 5 6

1 2 3 4 5 6

1 2 3 4 5 6

1 2 3 4 5 6

1 2 3 4 5 6

1 2 3 4 5 6

1 2 3 4 5 6

31 输入5数,倒序输出

32 不用条件语句计算各分数段人数

33 约瑟夫环问题,max人围成一圈,每数到jump,则该人出圈,直至所有人全部出圈为止 试求出圈顺序

34 约瑟夫环问题:

编号为 1,2,3,,N 的N个人按顺时针方向围坐一圈,每人持有一个密码(正整数)从指定编号为 1 的人开始,按顺时针方向自 1 开始顺序报数,报到指定值M时停止报数,报第M的人出列,并将他的密码作为新的M值,从他在顺时针方向的下一人开始,重新从 1 报数,如此类推,直至所有人全部出列为止试编一程序求出列顺序,其中 N<=30,N及密码数从键盘输入

35 编制一程序,要求输出20个数字(0-9),然后统计出在这个数组中相临两数字对出现的次数,如:0,1,5,9,8,7,2,2,2,3,2,7,8,7,8,7,9,6,5,9则程序得到7,8这一数字对出现次数为2;而8,7这一数字对出现次数为3

36 163 如图: 7 个学生按顺时针

① 方向手拉手围成一圈,并顺

172 ⑦ ② 170 序编号 ① ⑦, 用一

164 ⑥ ③ 160 个程序描述这 7个人按身高

167 ⑤ ④ 168 由矮到高重新排列面向内手

拉手的位置关系

图中小圈内的数字为编号, 小圈外的数字为各人的身高

37 读入若干个数,滤掉中值为20的数

38 任意输入N，求数列1,1/2,2/2,1/3,2/3的前N项。

39 将18k的自然数表示成2k行,要求奇数在下,偶数在上(k>0) k=4,则输出: 2 4 6 8

1 3 5 7

10 12 14 16

9 11 13 15

18 20 22 24

17 19 21 23

26 28 30 32

25 27 29 31

40 打印数字螺旋方阵,这个数字方阵的特点是:数字从外圈向里圈按自然数顺序转圈递增,从左上角的1到中心位置的NN为止,这里的N正好是方阵的行数或列数

41 编写一过程, 读入一个实型表示的度数,将其变成度,分,秒并显示

42 编一过程, 打印直方图,直方图为4行,每列表示1%

43 编写一个函数, 返回一正整数的倒序数字

44 编写一个过程, 倒序输出一正整数每位数字

45 幻方(奇阶和4的倍数阶)

46 打印由1——NN组成的NN的螺旋方阵 (N<=50)

N=4

7 8 9 10

6 1 2 11

5 4 3 12

16 15 14 13

47 验证任意自然数的阶乘均可表示为任意个素数的乘积的形式表示方法:

例如: 5!=222345

48 以输入的自然数N作为行数, 打印杨辉三角形

49 求出输入的N个自然数的最大公约数

50 N 个人进入会场开会(场内只有 N 个坐位), 本应对号入坐,可是N个人全都坐错了位置, 编程输出全都坐错了位置的所有可能坐法,并累计总数,N由键盘输入

51 求B/A+D/C结果表示成最简分数

52 求I!+J!+K!,其中I,J,K由键盘输入

53 求N!

54 将十进制数变为等值二进制数字

55 根据键盘输入的两个数G和H,求出[G,H]中的所有质数如果G<=2或G>H则要求重新输入

56 用递归方法求幂函数mn

57 跳马问题,55方阵,从左上角出发,跳遍所有格

58 一梯子有N格,小明上梯子有时一步上1格,有时一步上2格,编一程序,对任意输入的自然数N,打印出上梯子的所有可能的上法,并指出一共有多少种上法

59 第 13 届世界杯足球赛进入前八名的国家:

ARGENTINA(阿根廷),ENGLAND(英格兰),SPAIN(西班牙),BELGIUM(比利时)

GERMANY (西 德),MEXICO (墨西歌),FRANCE(法 国),BRAZIL (巴 西)

这八个国家的英文名藏在一个字块中:

A M U I G L E B P

P R W Y U B W R Y 需要设计一个程序查找这八个

W V G S T E X A N 国家的第一个字母所在的行和列以

Q N Q E C Y M Z A 及字母的走向字母的走向规定为

H O R N N Z E I M 八个方向,分别用八个字符串加以

W P A G L T X L R 标注,如图:

J R M L K J I L E UP LEFT UP UP RIGHT

F S P A I N C N G LEFT RIGHT

A K W N G F O I A BOEN LEFT DOWN DOWN RIGHT

B P J D C D E H J

要求按国名字符的先后次序打印查找结果, 输出格式规定如下:

NAME(国名) ROW(行) COL(列) DIRECTION(方向)

60 如果一个自然数N写在每个自然数之后则得到一个新数,它们都能被N整除 请找出

61 编一过程READOCAL,读入八进制序列,转换成正整数

62 设计一程序,要求在1到30的数中,读入一个数字,列出它的平方,立方和它本身都含有数字D的数,例如1,则11,121,1331都是这样的数

63 判断一数是否回文数

64 设计一个递归函数计算一个自然数有多少种加表示法

例如:5的加表示法有如下 7 种:

5,4+1,3+2,3+1+1,2+2+1,2+1+1+1,1+1+1+1+1

65 设计一个计算Ackerman函数的函数说明Ackerman函数定义为:

Ack(0,n)=n+1 (n>=0)

Ack(m,o)=Ack(m-1,1) (m>=1)

Ack(m,n)=Ack(m-1,Ack(m,n-1) (m,n>=1)

66 10数已排好序,现要插入一新数,使得新数列仍为排序数列

67 设p(x)是十进制整数x的所有数码的乘积,如整数12 的p(x)值为12=2 试求使下式成立的一切正整数: p(x)=x2-10x-22

68 识别字符串abababab,符合此规律的字符串,输出true,否则输出false,字符串总长度为N

69 编写布尔函数,以函数f为自变量,如果在x=0,01,02,0310时,f(x)均为正,则布尔函数值为true,否则为false

70 在1( )2( )3( )4( )5=( )中填入+,-,及合理数字,使之成为合理等式

71 在1()2()3()4()5()6()7()8()9=S中填入加减号使式子成立

72 在下面算式○中填入加号或减号,使算式结果等于键盘输入的S(S<200的自然数,且 S 是 9 的倍数)如果某个○不填符号,则将前后两个数字连成一个数(如:第一个○不填符号,即读成12),不允许相邻的两个○都不填符号如果对S有多种填法,必须全部填出,如果找不到填法,则打印\'NO!\'

1○2○3○4○5○6○7○8○9=S

73 有如图方阵:

R A D A R 试从其中任意R出发,找出产生RADAR

A D A R A 的路线打印每一种方案

D A R A D

A R A D A

R A D A R

74 求1到500之间本身和它二进制全是回文数的数

75 计算s除以1992后的商及余数(利用了字符串)

76 高精度加法

77 高精度乘法

78．对于任意输入的字符串判定其数据类型

79 对于任意N个数,经过处理,要求奇数在前,偶数在后,找所有排法

80有一个火车调度如图:

出口 -----\\ /------ 入口 有5列火车分别编号1,2,3,4,5

-----\\ \\/ /------ 1,2,3,4,5 依次排列于入口处,调度员可以

\\ / 在任意时刻将入口处的头一列

| | 火车拉入车站也可将最后进入

| | 车站的那列火车拉至出口处

车站

编程要求: 1模拟调度员的工作,使所有入口处的火车在出口处重新排列;

2打印出所有的火车在出口处的可能次序;

3若入口处的火车进一步增加到 N 列呢

81 设 X 为一个一维整数数组,其元素由1--N之间的所有整数随机排列,数组下标上限N由键盘输入 设计程序对数组X 的元素按如下定义的打印规则P打印:

(1) 如果 X 为空数组,打印"EMPTY";

(2) 如果 X 的长度是 1,打印出 X 的这个元素值;

(3) 如果 X 的长度大于1,设a是X的最小元素,B和C分别是a的左边元素和右边元素组成的子数组;

(4) 对B,C的所有元素按(1)(2)(3)规则处理,直至数组长度为1 为止

打印规则 P 将 X 数组的所有元素按上述处理原则打印,格式如下:

a

L:B(L 表示 a 的左边)

R:C(R 表示 a 的右边)

例如: X=(4,3,5,1,2),则打印成:

1

L: 3

L: 4

R: 5

R: 2

上述结果表示,数组X的最小元素为 1,1的左边元素组成的子数组B=(4,3,5) 而B的最小元素为 3, 3的左边元素为 4,右边元素为 5; 1的右边元素组成的数组为C=(2),只有一个元素

82 要求设计一个程序,在每行的字间插入适当空白,使得所有行都在同一列结束例如:

OPEN TOP COVER

TRACTOR FIXING RELEASE

在插入空白后变成:

OPEN TOP COVER

TRACTOR FIXING RELEASE

在每行字间插入空白时除了右端需对齐外,还需满足:

(1) 在不同的相临字间的空格最多相差 1;

(2) 对偶数(奇数)行, 所必须出现的空格出现在右端(左端)

83 对键盘输入的任意字符串,比较其相临的每两个字符,相同则输出+,不同输出-,再对新生成的+,-串作同样处理,直至剩一个字符为止

输入: 101101

则输出: --+--

+--+

-+-

--

+

84 有 NM (N列M行)张邮票连在一起,但其中第T张被挖掉了

举例:下面是45的邮票情况,其中第 13 张被挖掉了,

┌—┬—┬—┬—┐ 现在要求从这些邮票中撕出4张连在一起的邮

│ 1│ 6│11│16│ 票如1,2,3,4或1,2,6,7或 1,2,6,11等,

├—┼—┼—┼—┤ 问符合条件的4张相连的邮票有多少种撕法

│ 2│ 7│12│17│ (注:1,2,3,4 与2,3,4,5看作不同撕法)

├—┼—┼—┼—┤ 要求编写一个通用程序,并按如下格式打印:

│ 3│ 8│ │18│ 输入: 撕几连张

├—┼—┼—┼—┤ 邮票形状 N,M=

│ 4│ 9│14│19│ 被挖掉的邮票位置 N1,N2=

├—┼—┼—┼—┤ 输出: 打印所有撕法及总方案数

│ 5│10│15│20│

└—┴—┴—┴—┘

85 高精度乘方

86 有一个 NN (N为偶数)的图形,请你用 NN/2 个长为 2,宽为1 的长方块,将它全部覆盖,编程找出所有盖法要求每一种盖法不能重复,这里的重复是指经过旋转一个角度,或反过来时相同,输出最好用图形,也可用别的方式

87 MN 矩阵的各顶点随机填 0 和 1, 找出第一个四顶点值相同且面积最小的矩形

88 输入任一单词,统计其中元音和辅音字母出现的次数

89 设有一集合类型为set of 1n,n是主程序中用const说明的整数,试编一过程求出集合元素的个数

90 编一函数,决定一给定字符是字母,数字,空格,标点符号或其它符号

91 编一函数,若传递给它的整数仅包含数字1,3,5,7,9,则返回true,否则返回 false

92．用筛法求素数(255以内)

93 将十进制数N转化为二进制,并将1的所在位数存于集合

94．城市路线问题(如图) ,寻找最短路线图中括号内为里程数

⑽

┏━━━━━━━━━━┓

┃ ⑺ ┃

⑺┏━━━━B━━━━━━┓ ┃

┃ ┃ ┃ ┃

┃ ┏━━╋━━C━━━┻━┓ ┃

┃⑹┃ ┃ ┃ ┃ ┃

┃ ┃ ┃ ⑼┃ ⑸┃ ┃

A ━┫ ┃ ┃ ┃ ┃

┃ ┗━━╋━━╋━━━━━━D┫

┃ ⑽ ┃ ┃ ┃

┃ ┃ ┃ ┃

┃ ┗━━┻━━━━━┓ ┃⑹

┃ ⑽ ┃ ┃

┗━━━━━━━━━━━━━E━┛

(13)

95 一笔画问题 找出一笔画遍全图的所有方法

96 数码管问题找每两个位数字的数码笔画相差一的五位数

1

┌—┐

2│ │3

├ 4┤

5│ │6

└—┘

7

97 四色原理问题

98 表达式求值( 包括+,-,,/,^,(,) )

99 有一种绝对回文数,其十,二进制均为回文,请打印出1--500之间的绝对回文数(二进制最前面的0不能算)例如99(1100011)即是。

100 一人带狼,羊,白菜过河,狼吃羊,羊吃白菜,河中只有一条船,此人一次只能带一物过河用最少步全部过河

两个问题：

1、Integer太小了，数据早就爆了；

2、栈的调用过头了，“exitcode = 201”的意思就是栈溢出。

事实上，阿克曼函数的值是极大的。

Ackermann(0,n)=n+1

Ackermann(1,n)=n+2

Ackermann(2,n)=2n+3

Ackermann(3,n)=2^(n+3)-3

Ackermann(4,n)=2^2^2^……^2-3，乘幂中共有n+3个2。

当m≥4，Ackermann函数的增长快得惊人。Ackermann(4,0)=13，Ackermann(4,1)=65533，Ackermann(4,2)=2^65536-3有19729位，而Ackermann(4,3)则即使是位数也不易估计。Ackermann(5,0)=65533，Ackermann(5,1)=Ackermann(4,65533)……

针对于小数据，你的程序没问题。