python – Scipy – 如何进一步优化随机梯度下降的稀疏矩阵码

概述我正在使用Scipy的稀疏矩阵实现推荐系统的随机梯度下降算法. 这是第一个基本实现的样子： N = self.model.shape[0] #no of users M = self.model.shape[1] #no of items self.p = np.random.rand(N, K) self.q = np.random.rand(M, K) rows 我正在使用Scipy的稀疏矩阵实现推荐系统的随机梯度下降算法.

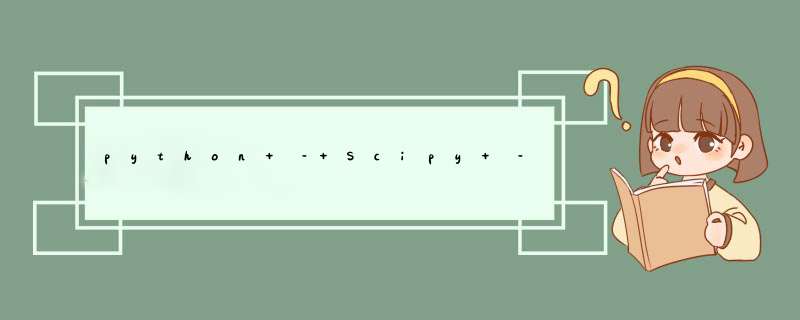
这是第一个基本实现的样子：

N = self.model.shape[0] #no of users    M = self.model.shape[1] #no of items    self.p = np.random.rand(N,K)    self.q = np.random.rand(M,K)    rows,cols = self.model.nonzero()            for step in xrange(steps):        for u,i in zip(rows,cols):            e=self.model-np.dot(self.p,self.q.T) #calculate error for gradIEnt            p_temp = learning_rate * ( e[u,i] * self.q[i,:] - regularization * self.p[u,:])            self.q[i,:]+= learning_rate * ( e[u,i] * self.p[u,:] - regularization * self.q[i,:])            self.p[u,:] += p_temp

不幸的是,我的代码仍然很慢,即使是一个小的4×5评级矩阵.我在想这可能是由于循环的稀疏矩阵.我尝试使用花哨的索引来表达q和p的变化但是因为我仍然是scipy和numpy的新手,我无法想出更好的方法来做到这一点.

你有没有关于如何避免明确地迭代稀疏矩阵的行和列的指针？

解决方法 我差点忘了关于推荐系统的一切,所以我可能会错误地翻译你的代码,但你在每个循环中重新评估self.model-np.dot(self.p,self.qT),而我几乎确信它应该被评估一次每一步.

然后看起来你手工进行矩阵乘法,可能会加速直接矩阵多重复制(numpy或scipy会比你手动更快),类似的东西：

for step in xrange(steps):    e = self.model - np.dot(self.p,self.q.T)    p_temp = learning_rate * np.dot(e,self.q)    self.q *= (1-regularization)    self.q += learning_rate*(np.dot(e.T,self.p))    self.p *= (1-regularization)    self.p += p_temp

总结

以上是内存溢出为你收集整理的python – Scipy – 如何进一步优化随机梯度下降的稀疏矩阵码全部内容，希望文章能够帮你解决python – Scipy – 如何进一步优化随机梯度下降的稀疏矩阵码所遇到的程序开发问题。

如果觉得内存溢出网站内容还不错，欢迎将内存溢出网站推荐给程序员好友。