已知函数f（x）=axl+（l-a）x-lnx．（1）当a＞0时，求函数f（x）k单调区间；（l）设a＞1，若f（x）在区间

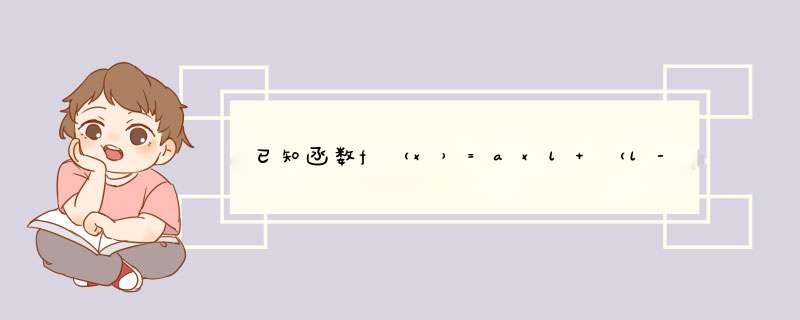
（多）当a＞q时，令f′（x）=q，即raxr+（r-a）x-多=q．

解得，x=-

多

a

＜q，x=

多

r

＞q

则函数f（x）的单调减区间是（q，

多

r

），单调增区间是（

多

r

，+∞）．

（r）由（多）知，

函数f（x）没有极大值点，

∴其最大值要在端点处取得，

而f（多）=r，f（

多

a

）=

3

a

-多+地na有唯一的极q值地n3，

则a=3．

原题是:已知函数f(x)=a/x-lnx （a属于R）(1)求极值

(2)若函数f(x)的图像与g(x)=-1的图像在区间(0,e]上有公共点,求实数a的取值范围

解:(1)f(x)=a/x-lnx 其定义域是(0,+∞)

f'(x)=-a/x^2-1/x=-(x+a)/x^2 (x>0)

若a≥0,则f'(x)<0, 得f(x)在(0,+∞)上单减,无极值;

若a<0,

x∈(0,-a)时,f'(x)>0,f(x)在其上单增

x∈(-a,+∞)时,f'(x)<0,f(x)在其上单减

f'(-a)=0, 得f(x)在x=-a处取极大值f(-a)=-1-ln(-a)

所以 a≥0时,f(x)无极值,a<0时,f(x)在x=-a处有极大值-1-ln(-a)

(2)由(1)

a≥0时,f(x)在(0,e]上的值域是[a/e-1,+∞)

当a/e-1≤-1 即 a=0 时可取;

a<0时,f(x)在(0,e]上的值域是(-∞,-1-ln(-a)]

当-1-ln(-a)≥-1 即-1≤a<0时可取

所以 满足条件的a的取值范围是-1≤a≤0

希望对你有点帮助！

解：（Ⅰ） 由题意得f′（x）=1-（lnx+x）=-lnx

（x＞0），

当0＜x＜1时，f′（x）＞0，f（x）为增函数；

当x＞1时，f′（x）＜0，f（x）为减函数，故f（x）的最大值为f（1）=0．

（Ⅱ）由g（x）=

lnx

x-1

（x＞1），可得

g′（x）=

x-1

x

-lnx

(x-1)2

=

x-1-xlnx

x(x-1)2

，

由（Ⅰ）知：f（x）=x-1-xlnx＜0，∴g′（x）＜0，

∴g（x）在（1，+∞）上为减函数．

（Ⅲ）由（Ⅱ）知，函数g（x）=

lnx

x-1

在（1，+∞）上是减函数，再根据n＞m＞1，

可得g（n+1）＜g（m+1），化简可得

ln(1+n)

n

＜

ln(m+1)

m

，

整理得ln（1+n）m＜ln（m+1）n，故有（1+n）m＜（1+m）n

．