在函数极限定义中epsilon和delta哪个更小？？？ 谢谢

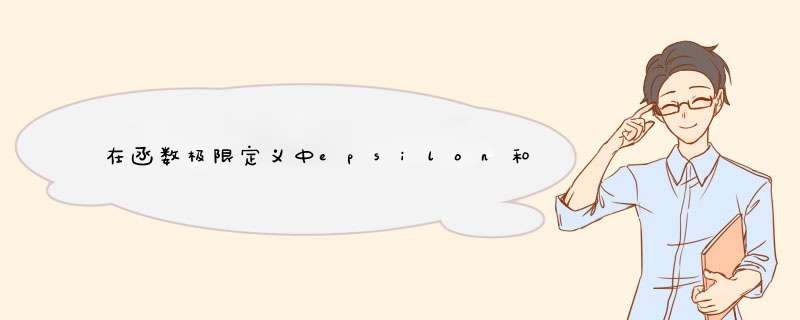
ε为任意一个小的正数，而δ是在某个点附近的点到该点的距离，一般要根据具体问题找出来，与ε并没有必然的大小关系。

由于一般只要求存在某个δ值，把它取得更小不影响定义，让它小于ε也是可以的。

ε的读音：/'epsila:n/。δ的读音：/'deltə/。

ε，希腊字母第五个字母，大写Ε，小写ε，拉丁字母的 E 是从ε变来。也可以指的是美式英语中使用的一个音标，即 bed 的 e 音。也是德国物理学家普朗克能量量子化假说中的最小能量值ε（叫能量子）。

δ（第四个希腊字母小写形式δ），Delta（大写Δ，小写δ），是第四个希腊字母。

扩展资料：

小写δ用处

用于：

1、共价键中的δ键（delta bond）

由两个d轨道四重交盖而形成的共价键称为δ键，可简记为“面对面”

δ键只有两个节面（电子云密度为零的平面）。从键轴看去，δ键的轨道对称性与d轨道的没有区别，而希腊字母δ也正来源于d轨道。

δ键常出现在有机金属化合物中，尤其是钌、钼和铼所形成的化合物。通常所说的“四重键”指的就是一个σ键、两个π键和一个δ键。

2、表示带电：δ-表示带负电，δ+表示带正电

3、数学中两个函数的名称：

克罗内克δ函数 （Kronecker delta）；狄拉克δ函数。

参考资料：

参考资料：

Enhancedwalltreatment是指壁面函数的一种，增强壁面函数！　　该方法不依赖于壁面法则，对于复杂流动尤其是低雷诺数流动问题很适合。该方法要求近壁面网格很密，y+接近于1，比low-Reynoldsnumbermodel要求的网格更密。　　对于epsilon方程的近壁面处理结合了速度分布双层模型和壁面增强处理函数。增强壁面处理使用传统的双层区域模型（整个计算域被划分为粘性影响区域和充分湍流区域）给边界层分区，然后给近壁单元指定湍流耗散率e和湍流粘度。增强型壁面函数的特点是用一个单一的壁面函数平滑地混合了对数层公式与层流公式，这样它的计算范围扩展到了全部近壁区域。　　增强壁面函数可用于以下湍流模型：　　（1）所有的基于epsilon的湍流模型（不包括二次RSM模型）　　（2）所有的w模型　　（3）对于SA模型，这一选项不可用。然而，这一模型对于壁面函数（y>15）及粘性子层网格（y15，要么y<2

楼上二位的证明方法都有问题，以下才是严格的证明。

证明：用反证法，设

lim

(x趋于a)

f'(x)

=

L，就是要证

L

=

f'(a)，那么我们先假设L

>

f'(a)。

如此一来，取L'

=

(L+f'(a))

/

2

>

f'(a)，根据函数极限的定义，对于

epsilon

=

(L-f'(a))/2

>

0，存在一个x的邻域

delta(x)，使得在这个邻域内的任意一个x，都有，

|

f'(x)

-

L

|

<

epsilon,

推出

f'(x)

>

L

-

epsilon

=

L'。

然后考虑在a点导数的定义：

lim

(x趋于a)

[f(x)

-

f(a)]

/

(x-a)

=

f'(a)，

考虑闭区间

[a,x]

（或者

[x,a]，取决于从哪个方向趋近于a，不过无所谓的），由于函数在该闭区间上连续，在开区间

(a,x)上可导，故根据拉格朗日微分中值定理，存在

c

属于

(a,x)，使得

[f(x)

-

f(a)]

/

(x-a)

=

f'(c)，

接着，由于当x趋于a时，

c也是趋于a的，所以最终，c一定会进入到刚才所说的x的邻域

delta(x)（注意我的epsilon

和邻域都已经取定了，对于固定的一个区间，只要c充分接近a，就一定会进入到这个区间），到那个时候，就总是有

f'(c)

>

L'，这样一来，当c趋于a时，由于函数极限的保号性，就有

f'(a)

>=

L'

>

f'(a)，这显然是一个矛盾。

同理，你也可以证明，当L

<

f'(a)时也会出现矛盾，L'的取法还是一样，

epsilon

你取

(f'(a)

-

L)/2即可。保证可以证的出来，不是一楼说的有问题。

还有问题可以追问。

按极限的定义，可以取 epsilon=|a0|/2, 那么存在 M>0 使得 x>M 时 | f(x)/x^n - a0 | < epsilon 恒成立

f(x)/x^n 到 a0 的距离不超过 |a0|/2, 而 0 到 a0 的距离只有 |a0|, 所以 a0 和 f(x)/x^n 都在 0 的同侧

这些都是基础知识，最好是先好好看教材，不要急于看教辅

你证明了f(x)在x=0处连续，但写法不够好，你的写法适合打草稿分析，分析完之后正式书写时最好是按照定义“对任何epsilon>0, 取delta=epsilon^{1/2}, 当|x-0|<delta时|f(x)-f(0)|<epsilon”这样的顺序来书写。

完整来讲你还应该证明f(x)在其它点都不连续。不过我建议如果没必要的话就不要用定义证明，可以用连续的性质。比如令g(x)=1/x^2, 如果f(x)在某个非零点x=c处连续，g(x)也在x=c处连续，就得到D(x)=f(x)g(x)也在x=c处连续，矛盾。

x=0处的连续性其实也不需要用epsilon-delta这样的语言，直接利用极限的性质(无穷小量乘以有界量)得到f(x)在x->0时的极限为0, 等于f(0)，从而得到x=0处连续。