求函数:f(x)=(x-1) ³√x² 的极值，求解题详解过程，谢！

求函数f(x)=(x-1) ³√x² 的极值

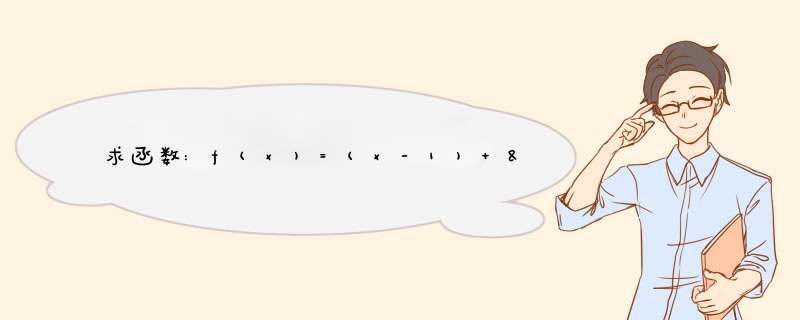
解：令f'(x)=x^(2/3)+(2/3)(x-1)x^(-1/3)=[3x+2(x-1)]/[3x^(1/3)]=(5x-2)/[3x^(1/3)=0

得唯一驻点x=2/5；x<2/5时f'(x)<0；x>2/5时f'(x)>0；故x=2/5是极小点。

极小值=f(2/5)=(2/5-1)(2/5)^(2/3)=-(3/5)[(2/5)^(2/3)]

无极大值。

本题另解(初二的二次方程知识)：

本题通用方法：全微分；本题步骤：

将所有条件等式全微分

用dz表示dx、dy

对要求极值的函数全微分，并将dx、dy用dz的表达式代入

由dz的系数(含x、y、z) = 0并联立条件解得稳定点

求稳定点的函数值并比较即可得极值；

本题完整解题过程：

虽然很多人点赞，但是踩的人也不少，

本题的解法可以用构造法，构造一个新的函数，但是大家看看网友“共同探讨55”的解题，满满一大篇，还离结果远着呢，而本人解法就 5 行，大家比较比较吧，还别说本人给出了一个更加简单的用初中二年级知识求解的方法，

本人微积分学的是江泽坚的数学分析，解题的理论依据，完全没有问题，

关于条件极值，变量 x、y、z，是有条件约束的，不是独立的变量，有一个条件，就可以减少一个变量，有两个条件就可以减少两个变量，这里有两个条件，所以问题的实质，求关于x、y、z 函数的极值，实际上就是求某一个变量的函数的极值，

如果还有人想踩，踩之前，应该把你们更高明的解法亮出来，否则算什么呀，

本解答经过修改、补充、完善。

求导了，如果有极值，那么导函数的方程一定有根，否则无根

f’（x）=3x^2+2ax+b

令f'(x)=0

方程无根，则无极值，判别可求得4a^2-12b<0,得到a^2<3b

一个极值，方程一个根，即a^2=3b

两个极值是a^2>3b

不用二阶求导的，没有意义，二阶等于0的点是拐点，根函数的极值点无关啊！

求z=x³+y³-3xy的极值

解：令∂z/∂x=3x²-3y=0，即x²-y=0①；∂z/∂y=3y²-3x=0，即y²-x=0②;

①②联立解得驻点M(0，0)；N(1，1)；

对每个驻点求出二阶偏导数的值A，B，C

A=∂²z/∂x²=6x；B=∂²z/∂x∂y=-3；C=∂²z/∂y²=6y;

驻点M(0，0): A=0，B=-3；C=0；B²-AC=9>0，故M不是极值点；

驻点N(1，1): A=6；B=-3；C=6；B²-AC=9-36=-27<0；且A=6>0，故N是极小点。

极小值Z=Z(1，1)=1+1-3=-1

分别对x，y求偏导数：

得到 cosx -cos(x+y)=0

cosy-cos(x+y)=0

显然可以得到 cosx=cosy

所以有 y= 2kπ±x

再反代回第一个式子去，得到 cosx-1=0 或者 cosx=cos2x

得到 x=2kπ 或者 x=2kπ/3

再筛选一下可，得到需要的答案。 （也许会用到二阶偏导的那个行列式）