用卡诺图将逻辑函数Y=C+ABC化成最简的与或式!

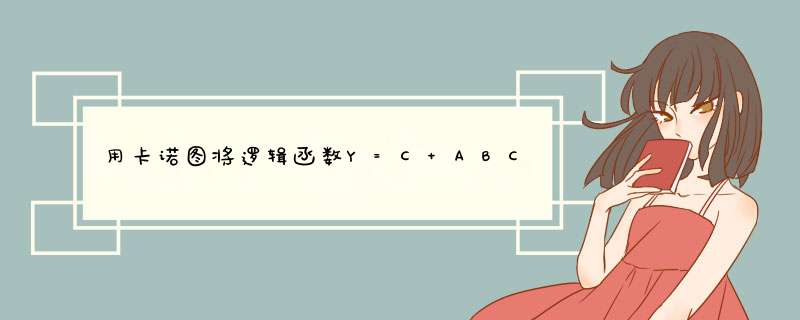
注释：红色的框框是ABC紫色的框框是C

卡诺图的要求一个框里至少有一个小格子未被其他的小格子覆盖,所确定的框框尽可能大所以我们选定紫色的大框框那么化简结果即为：Y=C;再验证一下：Y=ABC+C=C（AB+1）=C

Y=AB + AC + BC

求函数最简“与-或”表达式

（1）一般步骤：

第一步：作出函数的卡诺图

第二步：在卡诺图上圈出函数的全部质蕴涵项按照卡诺图上最小项的合并规律,对函数F卡诺图中的1方格画卡诺圈为了圈出全部质蕴涵项,画卡诺圈时在满足合并规律的前题下应尽可能大,若卡诺圈不可能被更大的卡诺圈包围,则对应的“与”项为质蕴涵项

第三步：从全部质蕴涵项中找出所有必要质蕴涵项在卡诺图上只被一个卡诺圈包围的最小项被称为必要最小项,包含必要最小项的质蕴涵项即必要质蕴涵项为了保证所得结果无一遗漏地覆盖函数的所有最小项,函数表达式中必须包含所有必要质蕴涵项

第四步：求出函数的最简质蕴涵项集若函数的所有必要质蕴涵项尚不能覆盖卡诺图上的所有1方格,则从剩余质蕴涵项中找出最简的所需质蕴涵项,使它和必要质蕴涵项一起构成函数的最小覆盖

f=a(-b)+b(-c)+(-b)c+(-a)b

=(a+c)(-b)+b[(-c)+(-a)]

分配率

=(a+c)(-b)+b[-(ac)]

后面化简就没有必要了，就是异或，与或了。

F = A'B+AC'+BC' = A'B+AC'+BC'（A+A'）

= A'B+AC'+ABC'+A'BC'

= A'B+A'BC' + AC'+ABC' = A'B（1+C'）+ AC'（1+B）;

=  A'B+AC'；