leetcode第 294 场周赛题解_C

leetcode第 294 场周赛题解 6074. 字母在字符串中的百分比原题链接算法标签模拟 AC代码

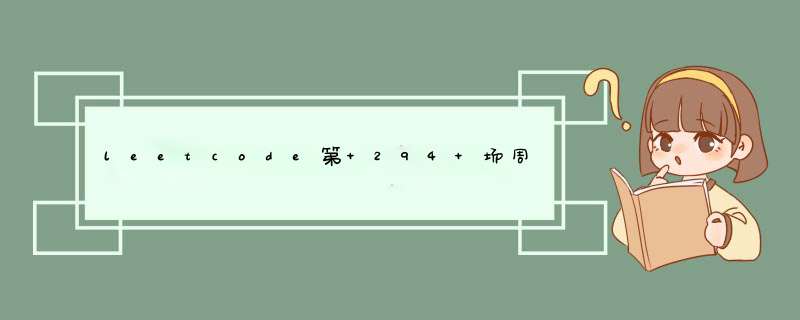
class Solution {
public:
    int percentageLetter(string s, char le) {
        int cnt=0;
        for(auto ss:s ){
            if(ss==le){
                cnt++;
            }
        }
        return cnt*100/s.size();
    }
};

6075. 装满石头的背包的最大数量原题链接算法标签排序枚举 AC代码

class Solution {
public:
    int maximumBags(vector& c, vector& r, int a) {
        vector v;
        for(int i=0;i=v[i]){
                a-=v[i];
                ans++;
            }
        }
        return ans;
    }
};

~~考虑最后依次是刚好用完还是不够，多虑了， WA两发~~

6076. 表示一个折线图的最少线段数原题链接算法标签高精度模拟 AC代码

class Solution {
    typedef long long ll;
public:
    int minimumLines(vector>& stockPrices) {
        sort(stockPrices.begin(),stockPrices.end());
        int n=stockPrices.size(),ans=1,i;
        for(i=1;i+1

 
WA代码 
class Solution {
public:
    const double exp = 1e-9;
    // 此处代码冗余 无需cmp函数
    static bool cmp(vector a, vector b){
        return a[0]>& s) {
        int ans=1;
         sort(s.begin(), s.end(), cmp);
        if(s.size()==2){
            return 1;
        }
        if(s.size()==1){
            return 0;
        }
        double f =(s[1][1]*1.0-s[0][1]*1.0)/(s[1][0]*1.0-s[0][0]*1.0);
        for(int i=1;iexp){
                f=(s[i+1][1]*1.0-s[i][1]*1.0)/(s[i+1][0]*1.0-s[i][0]*1.0);
                ans++;
            }
        }
        return ans;
    }
};
 
WA数据 

  
WA原因 即便更改数据类型为double， 返回值依旧为0， 依然存在精度丢失。 
TLE代码 
class Solution {
public:
    const double exp = 1e-10;
    // 此处代码冗余 无需cmp函数
    static bool cmp(vector a, vector b){
        return a[0]>& s) {
        int ans=1;
         sort(s.begin(), s.end(), cmp);
        if(s.size()==2){
            return 1;
        }
        if(s.size()==1){
            return 0;
        }
        // 分子*1000000000 防止精度丢失 
        double f =(s[1][1]*1.0-s[0][1]*1.0)*1000000000/(s[1][0]*1.0-s[0][0]*1.0);
        for(int i=1;iexp){
                f=(s[i+1][1]*1.0-s[i][1]*1.0)*1000000000/(s[i+1][0]*1.0-s[i][0]*1.0);
                ans++;
            }
        }
        return ans;
    }
};
 
TLE原因 上述代码理论使时间复杂度为O（n）, 与AC代码时间复杂度一致， 但由于设计大量乘除运算， 导致TLE。 
收获 
① . 对于vector二维数组排序， 默认所采用排序方式为将一维数据从首项至尾项将每一项排序。即 
bool cmp(vector a, vector b){
    return a[0]
 
②.若不用static修饰cmp函数， 将会报如下错误 
 
原因 所有在类内定义的非static成员函数在经过编译后隐式的为其添加了一个this指针参数！变为了： 
bool cmp(Solution *this, int a, int b)
 
而标准库的sort()函数的第三个cmp函数指针参数中并没有这样this指针参数，因此会出现输入的cmp参数和sort()要求的参数不匹配，从而导致了： 
error: reference to non-static member function must be called 
而static静态类成员函数是不需要this指针的，因此改为静态成员函数即可 
解决方法转自该处 
6077. 巫师的总力量和 
原题链接 
算法标签 单调栈 前缀和 
思路 

 题解转自该处 
AC代码 
class Solution {
public:
    int totalStrength(vector &strength) {
        const int mod = 1e9 + 7;

        int n = strength.size();
        vector left(n, -1); // left[i] 为左侧严格小于 strength[i] 的最近元素位置（不存在时为 -1）
        stack st;
        for (int i = 0; i < n; ++i) {
            while (!st.empty() && strength[st.top()] >= strength[i]) st.pop();
            if (!st.empty()) left[i] = st.top();
            st.push(i);
        }

        vector right(n, n); // right[i] 为右侧小于等于 strength[i] 的最近元素位置（不存在时为 n）
        while (!st.empty()) st.pop();
        for (int i = n - 1; i >= 0; --i) {
            while (!st.empty() && strength[st.top()] > strength[i]) st.pop();
            if (!st.empty()) right[i] = st.top();
            st.push(i);
        }

        long s = 0L; // 前缀和
        vector ss(n + 2); // 前缀和的前缀和
        for (int i = 1; i <= n; ++i) {
            s += strength[i - 1];
            ss[i + 1] = (ss[i] + s) % mod;
        }

        int ans = 0;
        for (int i = 0; i < n; ++i) {
            long l = left[i] + 1, r = right[i] - 1; // [l,r] 左闭右闭
            long tot = ((i - l + 1) * (ss[r + 2] - ss[i + 1]) - (r - i + 1) * (ss[i + 1] - ss[l])) % mod;
            ans = (ans + strength[i] * tot) % mod; // 累加贡献
        }
        return (ans + mod) % mod; // 防止算出负数（因为上面算 tot 有个减法）
    }
};
 
战绩 

 原创不易
 转载请标明出处
 如果对你有所帮助 别忘啦点赞支持哈
 					
										


					
						欢迎分享，转载请注明来源：内存溢出
原文地址: http://outofmemory.cn/langs/1294932.html

leetcode第 294 场周赛题解

发表评论

评论列表（0条）