洛谷P1216 2022.5.22 13:29

C：（100分）

我理解的大概原理：

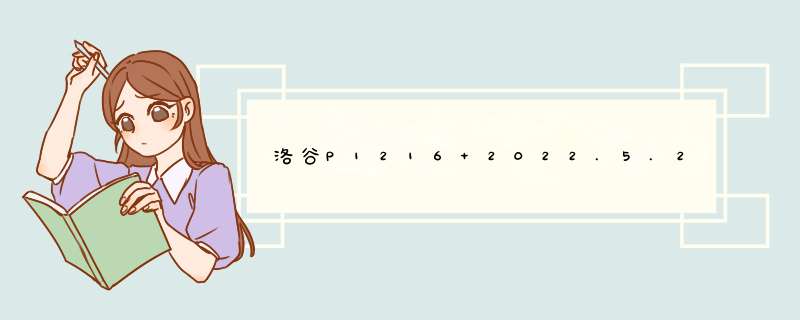
题目：“从最高点到底部任意处结束的路径，使路径经过数字的和最大”

也就是找下面其中的一条路线，然后把这条路线上的所有数加起来，找到和数最大的那条路线

然后当时我的第一想法是列出所有的路线，然后得出每条路线的和，比如：

7（塔顶）- 3 - 8 - 2 - 4 和为 24

7（塔顶）- 3 - 8 - 2 - 5 和为 25

............................

之后了解到了下面要说的算法，感觉简单了很多很多

这个算法的基本原理有两点：

1. 逆向思维，从塔顶开始弄

2. 比较 一个数A 与相连的两个数中哪个数最大，把这个最大的数加到A上

（我们可以从这金字塔看出，除去塔顶和塔底的数外，每个数对上面有一个数相连，对下面有两个数相连

以该图左下部分为例：

除去塔底的4 和 5

以2为例

2对上面只有一个数相连，为8

2对下面有两个数相连，为4 和 5

做一个判断，在4 和 5中选择最大的那个加到2上面，2变成7

右边也与左边一样

待塔底的所有数都比较完也选择相应最大的加到 塔底第二行上，第二行也重复上述步骤

最终汇聚到塔顶

最后只需要输出塔顶的数，就可以得到 “单独的一行,得到的最大的和”

（大概是这个样，可能说的不是很清楚，建议自己上机看监视过一遍）

）

#define _CRT_SECURE_NO_WARNINGS 1

#include 

#define biao_Max 1001

int biao[biao_Max][biao_Max] = { 0 };  //创建一个二维数组来储存 数字金字塔

int whoismax(int x, int y)
{
	return x > y ? x : y;
}


int main()
{
	int r = 0;  //正整数 r ,表示行的数目

	scanf("%d", &r);

	//把数字金字塔导入二维数组内
	for (int i = 0; i < r; i++)
	{
		for (int j = 0; j <= i; j++)
		{
			scanf("%d", &biao[i][j]);
		}
	}

	//算法主体
	for (int i = r - 2; i >= 0; i--)
	{
		for (int j = 0; j <= i; j++)
		{
			biao[i][j] += whoismax(biao[i + 1][j], biao[i + 1][j + 1]);
		}
	}

	printf("%d", biao[0][0]);

	return 0;
}

C++：（100分）

C++的话就是把自制的max函数换成了头文件自带的，然后修改了输入和输出，没什么大变化

#define _CRT_SECURE_NO_WARNINGS 1

#include 

#include 

using namespace std;

#define biao_Max 1001

int biao[biao_Max][biao_Max] = { 0 };  //创建一个二维数组来储存 数字金字塔

int main()
{
	int r = 0;  //正整数 r ,表示行的数目

	cin >> r;

	//把数字金字塔导入二维数组内
	for (int i = 0; i < r; i++)
	{
		for (int j = 0; j <= i; j++)
		{
			cin >> biao[i][j];
		}
	}

	//算法主体
	for (int i = r - 2; i >= 0; i--)
	{
		for (int j = 0; j <= i; j++)
		{
			biao[i][j] += max(biao[i + 1][j], biao[i + 1][j + 1]);
		}
	}

	cout << biao[0][0];

	return 0;
}

python：(100分）

python版的C语言，python中没有二维数组，就改用列表了

r = eval(input())

list1 = []

for i in range(r):
    list1.append(list(map(int, input().split(" "))))

for i in reversed(range(r - 1)):
    for j in range(i + 1):
        list1[i][j] += max(list1[i + 1][j], list1[i + 1][j + 1])

print(list1[0][0])