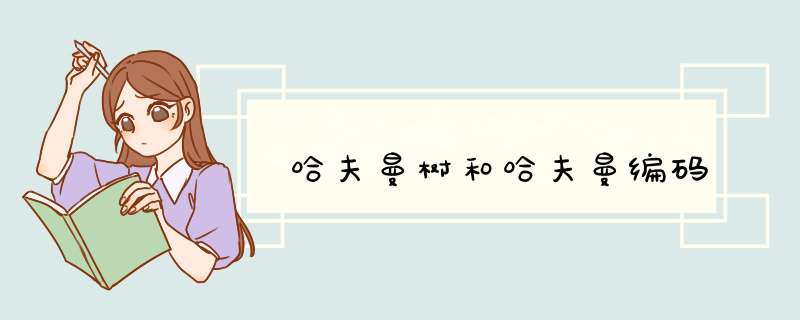
哈夫曼是也成最优二叉树,其主要思想是每次找最小的两个值作为树的最深层,剔除最小的两个值后加入两者和,再在其中找最小值直到剩下最后一个作为根节点。
构建haffman树:构建哈夫曼树 ,要准备一个2*n-1大小的结构体数组(n为叶子节点的个数),前n个数组放原始数据,后面n-1个数组放相加后的数据。因此第一个循环仅仅是赋值,作为叶子节点,没有左右孩子,所以赋值为-1,后面没有计算找到父节点,也赋值为-1,flag为是否相加过。
struct Tree //权重,是否访问过,父节点,左右孩子
{
int weight;
int flag;
int parent;
int leftchild;
int rightchild;
};
void HaffmanTree(int weight[], int n, struct Tree Haffman_Tree[])
{
int i, j, m1, m2, x1, x2;
for (i = 0; i < n * 2 - 1; i++)
{
if (i < n) Haffman_Tree[i].weight = weight[i];
else Haffman_Tree[i].weight = -1;
Haffman_Tree[i].parent = -1;
Haffman_Tree[i].flag = 0;
Haffman_Tree[i].leftchild = -1;
Haffman_Tree[i].rightchild = -1;
}
for (i = 0; i < n - 1; i++)//总节点数为2*n-1,n-1为未赋值的数量
{
x1 = x2 = 0;
m1 = m2 = M;
for (j = 0; j < n + i; j++)//随着父节点的增加,循环的次数也随着i的增加而增加
{
if (Haffman_Tree[j].weight < m1 && Haffman_Tree[j].flag == 0) //找到最小的数据,将原本的最小数据变成第二小
{
x2 = x1;
m2 = m1;
m1 = Haffman_Tree[j].weight;
x1 = j;
}
else if (Haffman_Tree[j].weight < m2 && Haffman_Tree[j].flag == 0) //找第二小的数据,只进入一次
{
m2 = Haffman_Tree[j].weight;
x2 = j;
}
}
Haffman_Tree[n + i].weight = Haffman_Tree[x1].weight + Haffman_Tree[x2].weight; //父节点的权重
Haffman_Tree[n + i].leftchild = x1, Haffman_Tree[n + i].rightchild = x2; //父节点的左右孩子
Haffman_Tree[x1].flag = Haffman_Tree[x2].flag = 1; //子节点的判断
Haffman_Tree[x1].parent = Haffman_Tree[x2].parent = n + i; //子节点的父节点
}
}
第二个双循环找最小的两个数据,原先只有n个数据,外循环只要找n-1次就行了,每相加一次,原来的结构体数组权重要更新一次(原先i>=n时weight=-1)要重新赋值,所以j的取值范围也要随着i的改变而改变。m1取最小值,m2取最大值,如果有比m1更小的,m1m2都更新。
哈夫树的构件表: 哈夫曼编码:最外循环指向的是所以叶子节点,从叶子节点开始往数组下发推,树往根上推,直到找到根节点,边找遍编码(while)。数组是从最后一个开始往前赋值的,而start记录最前面的位置,所以start每次都赋初值为n-1,每次编码都减一。最后下标后移一位。
struct Code //哈夫曼编码,记录哈夫曼编码的结束点,权重
{
int* bit;
int start;
int weight;
};
void HaffmanCode(struct Tree Haffman_Tree[], int n, struct Code Haffman_Code[])
{
struct Code* ptemp = new Code;
int i, j, iparent, ichild;
for (i = 0; i < n; i++) //对叶子节点进行哈夫曼编码
{
Haffman_Code[i].bit = new int[n];
ptemp->start = n - 1; //从最大的开始赋值
ptemp->bit = new int[n];
ichild = i;
iparent = Haffman_Tree[ichild].parent;
while (iparent != -1) //直到找到根节点,找到祖宗位置为止
{
if (Haffman_Tree[iparent].leftchild == ichild) //左孩子为0
{
ptemp->bit[ptemp->start--] = 0;
}
else //右孩子为1
{
ptemp->bit[ptemp->start--] = 1;
}
ichild = iparent; //孩子当爹
iparent = Haffman_Tree[ichild].parent; //爹找爹的爹
}
//赋值给Haffman_Code值
for (j = ptemp->start + 1; j < n; j++)
{
Haffman_Code[i].bit[j] = ptemp->bit[j];
}
Haffman_Code[i].weight = Haffman_Tree[i].weight;
Haffman_Code[i].start = ptemp->start + 1;
}
}
#include
#define M 100000
using namespace std;
struct Tree //权重,是否访问过,父节点,左右孩子
{
int weight;
int flag;
int parent;
int leftchild;
int rightchild;
};
struct Code //哈夫曼编码,记录哈夫曼编码的结束点,权重
{
int* bit;
int start;
int weight;
};
void HaffmanTree(int weight[], int n, struct Tree Haffman_Tree[])
{
int i, j, m1, m2, x1, x2;
for (i = 0; i < n * 2 - 1; i++)
{
if (i < n) Haffman_Tree[i].weight = weight[i];
else Haffman_Tree[i].weight = -1;
Haffman_Tree[i].parent = -1;
Haffman_Tree[i].flag = 0;
Haffman_Tree[i].leftchild = -1;
Haffman_Tree[i].rightchild = -1;
}
for (i = 0; i < n - 1; i++)//总节点数为2*n-1,n-1为未赋值的数量
{
x1 = x2 = 0;
m1 = m2 = M;
for (j = 0; j < n + i; j++)//随着父节点的增加,循环的次数也随着i的增加而增加
{
if (Haffman_Tree[j].weight < m1 && Haffman_Tree[j].flag == 0) //找到最小的数据,将原本的最小数据变成第二小
{
x2 = x1;
m2 = m1;
m1 = Haffman_Tree[j].weight;
x1 = j;
}
else if (Haffman_Tree[j].weight < m2 && Haffman_Tree[j].flag == 0) //找第二小的数据,只进入一次
{
m2 = Haffman_Tree[j].weight;
x2 = j;
}
}
Haffman_Tree[n + i].weight = Haffman_Tree[x1].weight + Haffman_Tree[x2].weight; //父节点的权重
Haffman_Tree[n + i].leftchild = x1, Haffman_Tree[n + i].rightchild = x2; //父节点的左右孩子
Haffman_Tree[x1].flag = Haffman_Tree[x2].flag = 1; //子节点的判断
Haffman_Tree[x1].parent = Haffman_Tree[x2].parent = n + i; //子节点的父节点
}
}
void HaffmanCode(struct Tree Haffman_Tree[], int n, struct Code Haffman_Code[])
{
struct Code* ptemp = new Code;
int i, j, iparent, ichild;
for (i = 0; i < n; i++) //对叶子节点进行哈夫曼编码
{
Haffman_Code[i].bit = new int[n];
ptemp->start = n - 1; //从最大的开始赋值
ptemp->bit = new int[n];
ichild = i;
iparent = Haffman_Tree[ichild].parent;
while (iparent != -1) //直到找到根节点,找到祖宗位置为止
{
if (Haffman_Tree[iparent].leftchild == ichild) //左孩子为0
{
ptemp->bit[ptemp->start--] = 0;
}
else //右孩子为1
{
ptemp->bit[ptemp->start--] = 1;
}
ichild = iparent; //孩子当爹
iparent = Haffman_Tree[ichild].parent; //爹找爹的爹
}
//赋值给Haffman_Code值
for (j = ptemp->start + 1; j < n; j++)
{
Haffman_Code[i].bit[j] = ptemp->bit[j];
}
Haffman_Code[i].weight = Haffman_Tree[i].weight;
Haffman_Code[i].start = ptemp->start + 1;
}
}
int main()
{
int n, * weight, i, j;
cin >> n;
struct Tree* Haffman_Tree = new struct Tree[2 * n - 1];
struct Code* Haffman_Code = new struct Code[n];
weight = new int[n];
for (i = 0; i < n; i++)
{
cin >> weight[i];
}
cout << endl;
HaffmanTree(weight, n, Haffman_Tree);
/* for (int i = 0; i < 2 * n - 1; i++) //haffman树的构件表
{
cout <
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)