LeetCode刷题：532.数组中的K-diff数对

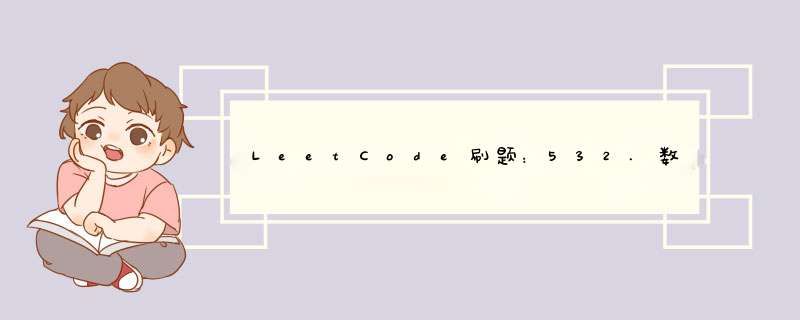
题目描述：

看到这个题目第一眼就：排序+回溯+剪枝，统计最后结果数
好消息是根据这个思路写出来了，成功解题
坏消息是因为下标问题卡了一个小时，压死骆驼的最后一根稻草
看到官方解答，官方思路：排序+二分查找，自闭了

排序+回溯+剪枝思路如下：
我寻思这个相当与从数列中挑选两个数的全排列吧，把一对一对的组合全写出来，然后挑选合格的，剪枝 *** 作可以去除一下重复的数组以及明显val值会大于K的数组。这样呢，剪枝之后会比暴力求解时间复杂度低一些。

之前看到一个人说过，回溯和暴力循环差不多，只是回溯通过剪枝的技巧，去除一些重复的分支，就是少循环几次，通过剪枝 *** 作降低时间复杂度。
因此如何剪枝是重点。
首先对数组排序，目标数组 nums = [1,3,1,4,5],k =0
剪枝一： 排序后[1,1,3,4,5]，对第一个1进行全部组队的结果，和用第二个1进行全部组队的结果是一样的，因此就把第二个1的分支剪掉
剪枝二
因为数组是排序后的，若3-1>k,那么3之后的数对也肯定大于k，就没必要计算后面的数对，进行剪枝

class Solution {
     public int findPairs(int[] nums, int k) {
        int n = nums.length;
        if (n<2){
            return 0;
        }
        // 用来存储所有符合要求的结果
        List<List<Integer>> list = new ArrayList<>();
        // 数组对，符合要求的才会添加到list
        List<Integer> path = new ArrayList<>();
        // 排序
        Arrays.sort(nums);
        dfs(0,n,nums,k,path,list);
        int ans = list.size(); // 返回最终有数组对数
        return ans;
    }
    public void dfs(int index,int n,int[] nums,int k,List<Integer> path,List<List<Integer>> list){
    // 当前路径中 已经添加了两个数值，对其进行是否符合要求的判断
        if (path.size()==2  ){
        //符合要求，添加进list ,返回
            if (path.get(1)-path.get(0)==k){
                list.add(new ArrayList<>(path));
                return;
            }else {
            // 否则，直接返回
                return;
            }
        }
        for (int i =index;i<n;i++){
        // 剪枝1
            if (i>index && nums[i]==nums[i-1]){
                continue;
            }
            // 剪枝2
            if (path.size()>0 && nums[i]-path.get(0)>k){
                break;
            }
            path.add(nums[i]);
            dfs(i+1,n,nums,k,path,list);
            path.remove(path.size()-1);
        }
    }
}

恐怕这道题目只有我一个人这样写吧 还是太菜，没想到其他思路。加油！

排序+二分查找
代码：

 public int findPairs2(int[] nums, int k) {
            int n = nums.length, res = 0;
            Arrays.sort(nums);
            for (int i = 0; i < n - 1; i++) {
                //重复的不计算，如果相同nums[i-1]已经计算过了
                if (i > 0 && nums[i] == nums[i - 1]) {
                    continue;
                }
                int target = nums[i] + k;
                //在[i+1,n-1]中找target
                int left = i + 1, right = n - 1;
                int ans = -1;
                while (left <= right) {
                    int mid = left + (right - left) / 2;
                    if (nums[mid] >= target) {
                        ans = mid;
                        right = mid - 1;
                    } else {
                        left = mid + 1;
                    }
                }
                //判断是否找到
                if (ans != -1 && nums[ans] == target) {
                    res++;
                }
            }
            return res;
        }