E(X)=nMN是离散型随机变量的公式，请问各个字母表示的是什么意思书上没看到，帮忙以下把

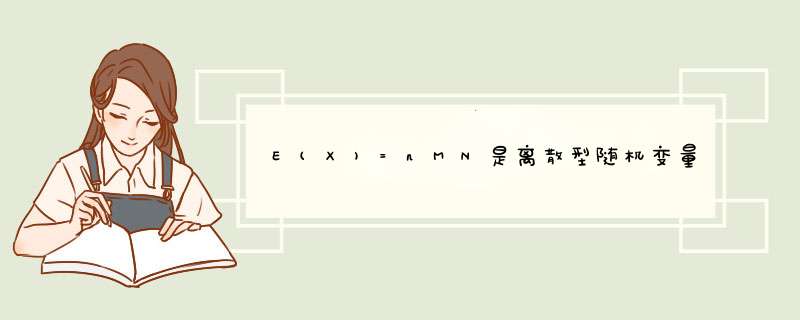
X是一个离散型随机变量，服从次数为n，成功概率为M/N的二项分布，记作： X ~ B(n, M/N)。

E(X)是X的期望，通过计算等于nM/N，即E(X)=nM/N

当然还有其它信息可以给你：

这个二项分布X ~ B(n, M/N)的方差是：

n(M/N)(1-M/N)

离散型随机变量X的取值为  ，  为X对应取值的概率，可理解为数据  出现的频率  ，则：。

其中E(x）为期望，∑为求和公式。

在概率论和统计学中，数学期望（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。

扩展资料：

数学期望的来历：

在17世纪，有一个赌徒向法国著名数学家帕斯卡挑战，给他出了一道题目：甲乙两个人赌博，他们两人获胜的机率相等，比赛规则是先胜三局者为赢家，一共进行五局，赢家可以获得100法郎的奖励。

当比赛进行到第四局的时候，甲胜了两局，乙胜了一局，这时由于某些原因中止了比赛，那么如何分配这100法郎才比较公平？用概率论的知识，不难得知，甲获胜的可能性大，乙获胜的可能性小。

因为甲输掉后两局的可能性只有(1/2)×(1/2）=1/4，也就是说甲赢得后两局的概率为1－(1/4)=3/4，甲有75%的期望获得100法郎；而乙期望赢得100法郎就得在后两局均击败甲，乙连续赢得后两局的概率为(1/2)(1/2)=1/4，即乙有25%的期望获得100法郎奖金。

可见，虽然不能再进行比赛，但依据上述可能性推断，甲乙双方最终胜利的客观期望分别为75%和25%，因此甲应分得奖金的10075%=75(法郎)，乙应分得奖金的的100×25%=25(法郎)。这个故事里出现了“期望”这个词，数学期望由此而来。

参考资料：

1首先需要打开excel表格，如下图。

2首先，找到一行并输入相应的权重，可以直接输入到最上面一行的中。

3找到公式-插入函数-sumproduct()，它可以在所有函数中找到。

4找到它之后，选择Array1和array2，它们分别是权重和 *** 作数。

5结果是你想要的值的加权和，如下图。

6有时，例如，当你需要大量计数时，两个变量都在变化。

7所以我们需要做一个变量变换。在这里，我们将重量输入到手册中，并手动编写公式。

8然后按Ctrl键将鼠标放置在框的右下角，您将看到它是自动计算的。

方法如下：

Cov(X,Y)=Σ(i=1->n) [Xi-E(X)][Yi-E(Y)] / {Σ(i=1->n) [Xi-E(X)]^2[Yi-E(Y)]^2}^05

离散型随机变量的方差：

D(X)=E{[X-E(X)]^2}(1)

=E(X^2)-(EX)^2(2)

（1）式是方差的离差表示法。

（2）式表示：方差=X^2的期望-X的期望的平方。

X和X^2都是随机变量，针对于某次随机变量的取值，例如：随机变量X服从“0-1”：

取0概率为q，取1概率为p，p+q=1则：对于随即变量X的期望E(X)=0q+1p=p。

同样对于随即变量X^2的期望E(X^2)=0^2q+1^2p=p。

所以由方差公式（2）得：D(X)=E(X^2)-(EX)^2=p-p^2=p(1-p)=pq。

方差统计

方差在统计描述和概率分布中各有不同的定义，并有不同的公式，在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。

以上就是关于E(X)=nM/N 是离散型随机变量的公式，请问各个字母表示的是什么意思书上没看到，帮忙以下把全部的内容，包括:E(X)=nM/N 是离散型随机变量的公式，请问各个字母表示的是什么意思书上没看到，帮忙以下把、离散型变量的数学期望如何计算、excel 离散系数怎么计算等相关内容解答，如果想了解更多相关内容，可以关注我们，你们的支持是我们更新的动力！