如何求树叶图形面积?

用两个四分之一圆面积之和减去正方形面积即可。
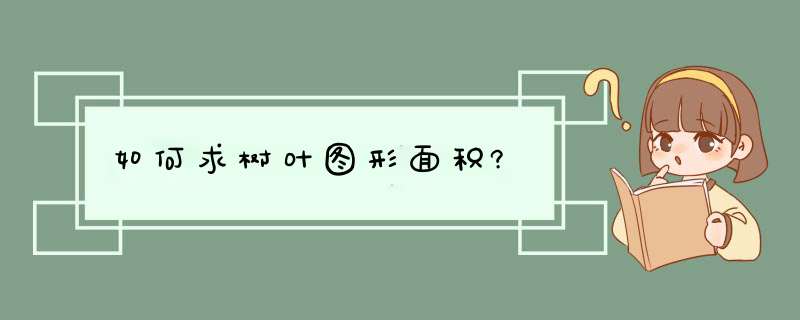
解：例如正方形边长为1厘米，则阴影面积：
314×1×1×1/4×2－1×1＝057（平方厘米）
边长为n，则算法是：
314×n×n×1/4×2－n×n

用两个四分之一圆面积之和减去正方形面积即可
例如正方形边长为1厘米,则阴影面积：
314×1×1×1/4×2－1×1＝057（平方厘米）
边长为n,则算法是：
314×n×n×1/4×2－n×n

描绘树叶，边的曲线函数用回归办法。有了曲边函数，就可以用定积分求面积。

D的面积，A是由曲线px^3在[0,1]的积分，即曲边梯形的面积，减去切线，x轴，x=1围城的直角三角形面积(p/6)得到的。

S=4∫∫(xy/a)dxdy

=(4/a)[∫(0->π/2)dθ][∫(0->a)(r^3sinθcosθ)dr

=a^3/2

扩展资料：

一般定理

定理1：设f(x)在区间[a,b]上连续，则f(x)在[a,b]上可积。

定理2：设f(x)区间[a,b]上有界，且只有有限个间断点，则f(x)在[a,b]上可积。

定理3：设f(x)在区间[a,b]上单调，则f(x)在[a,b]上可积。

定积分与不定积分看起来风马牛不相及，但是由于一个数学上重要的理论的支撑，使得它们有了本质的密切关系。把一个图形无限细分再累加，这似乎是不可能的事情，但是由于这个理论，可以转化为计算积分。

参考资料来源：百度百科-定积分

---