excel如何将一组数值的Y值求出？

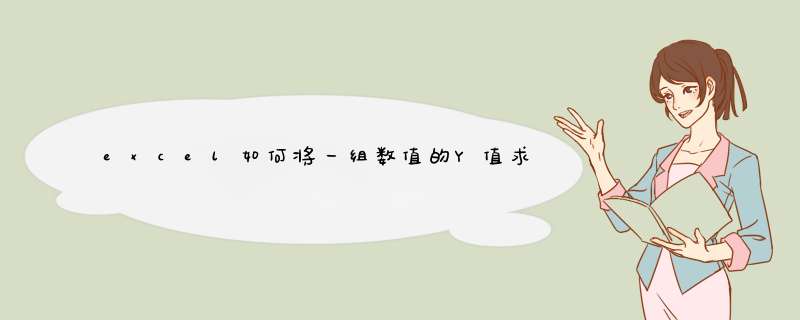
如图输出Y值的单元格为D7的话

D7输入 =46E6-7D6D6+00024D6+00388

只要改变图中D6的值(D6为变量χ)，Y的值会跟着改变即D7改变

单元格D7代表整个公式 y=46E-7X^2+00024X+00388 的输出结果

方法/步骤
第一步仍然是准备好我们需要的数据，纵向排列
首先计算Y的估计值，我们根据回归方程计算
在C2单元格里面输入“=048$B2-202108”，回车计算出结果，然后向下拖动生成所有点对应的y估计值
接着我们需要计算残差e，在D2单元格里面输入“=$C2-$A2”还是向下拖动生成残差列
然后计算残差的平方，在E2单元格里面输入“=D2^2”
做右侧空白区域选择一个单元格，比如M2，在单元格里面输入“=SUM(E2:E20)”计算残差的平方和
接下来我们计算x的平方，在F2单元格里面输入“=B2^2”向下拖动生成x的平方值列
同样在右侧找一个单元格，如M3，输入“=SUM(F2:F20)”回车
接下来我们计算估计误差
先在K2单元格计算出x的均值，输入“=AVERAGE(B2:B20)”
在K3输入需要计算得X值，比如这里的3000
在K5单元格里面输入“=SQRT($M$2/17(1/18+($K$3-$K$2)^2/$M$3))”回车输出误差值
如果计算得是置信区间的话，可以另外选择单元格输入“=SQRT($M$2/17(1+1/18+($K$3-$K$2)^2/$M$3))”
我们需要分别计算预测区间的上限和下限
在J9单元格里面输入“=$M$5-TINV(005,17)$K$5”回车，作为下限值
在K9单元格里面输入“=$M$5+TINV(005,17)$K$5”回车，作为上限值
7
接下来如果我们需要更换X的值，只需要在K3单元格里面重新输入X新的数值，然后回车，在J3和K3单元格就会计算出Y的预测区间的下限和上限。

1、列计算表，求∑x，∑xx，∑y，∑yy，∑xy。

2、计算Lxx，Lyy，LxyLxx=∑(x-xˇ)(x-xˇ)Lyy=∑(y-yˇ)(y-yˇ)Lxy=∑(x-xˇ)(y-yˇ)

3、求相关系数，并检验；r = Lxy /( Lxx Lyy)1/2

4、求回归系数b和常数a；b=Lxy /Lxxa=y - bx

5、列回归方程。

扩展资料：

根据最小平方法或其他方法，可以从样本数据确定常数项A与回归系数B的值。A、B确定后，有一个X的观测值，就可得到一个Y的估计值。回归方程是否可靠，估计的误差有多大，都还应经过显著性检验和误差计算。有无显著的相关关系以及样本的大小等等，是影响回归方程可靠性的因素。

如果只有一个自变量X，而且因变量Y和自变量X之间的数量变化关系呈近似线性关系，就可以建立一元线性回归方程，由自变量X的值来预测因变量Y的值，这就是一元线性回归预测。

如果因变量Y和自变量X之间呈线性相关，那就是说，对于自变量X的某一值

，因变量Y对应的取值

不是唯一确定的，而是有很多的可能取值，它们分布在一条直线的上下，这是因为Y还受除自变量以外的其他因素的影响。

这些因素的影响大小和方向都是不确定的，通常用一个随机变量(记为

)来表示。

使用Eviews很方便，点Eviews上面uick---------Estimate Equation,看看可决系数就可以了。
或者：（1）计算残差平方和Q=∑(y-y)^2和∑y^2，其中，y代表的是实测值，y代表的是预测值；
（2）拟合度指标RNew=1-(Q/∑y^2)^(1/2)
Rnew是最近才出现的用于判定非线性回归方程的拟合度的统计参数，现在我还没有看到它的中文名称。之所以用角标new就是为了和线性回归方程的判定系数R2、adjusted R2进行区别。在对方程拟合程度的解释上，Rnew和R2、adjusted R2是等价的，其意义也相同。
对线性方程：
R^2==∑(y预测-y)^2/==∑(y实际-y)^2，y是平均数。如果R2=0775，则说明变量y的变异中有775％是由变量X引起的。当R2＝1时，表示所有的观测点全部落在回归直线上。当R2=0时，表示自变量与因变量无线性关系。
拟合优度是指回归直线对观测值的拟合程度。度量拟合优度的统计量是可决系数（亦称确定系数）R^2。R^2的取值范围是[0，1]。R^2的值越接近1，说明回归直线对观测值的拟合程度越好；反之，R^2的值越接近0，说明回归直线对观测值的拟合程度越差。

在英文状态下同时按下shift+数字6键则可在β上面打出估计值的符号^了，则"β^"。

如果直接按数字6键，打出来的是数字“6”；如果在中文状态下按shift+数字6键，打出来的是省略号“……”；如果在英文状态下按shift+数字6键，打出来的是符号“^”。

键盘上按shift键则可直接切换中英文状态。

扩展资料：

键盘上一些常见符号的打法：

“！”符号：shift+数字1键；

“@”符号：shift+数字2键；

“#”符号：shift+数字3键；

“$”符号：shift+数字4键（英文状态）；

“￥”符号：shift+数字4键（中文状态）；

“%”符号：shift+数字5键；

“&”符号：shift+数字7键；

“”符号：shift+数字8键；

“（”符号：shift+数字9键；

“）”符号：shift+数字0键。

预测是指通过自变量x的取值来预测因变量y的取值。
1、平均值的点估计：实际上是对总体参数的估计是利用估计的回归方程，对于x的一个特定值x_{0}，求出y的平均值的一个估计值E(y_{0})。
2、个别值的点估计：对因变量的某个具体取值的估计是利用估计的回归方程，对于x的一个特定值x_{0}，求出y的一个个别值的估计值\hat{y}_{0}。

---