哪个大神有时间帮我对VRP问题用禁忌搜索算法编写一个lingo或者c语言可以

求最短配送路径的话 应该是TSP问题吧，不应该是VRP问题。

LINGO能很好地求解这两类模型，但用的整数规划原理或动态规划原理，不能用禁忌搜索。

禁忌搜索，就用C或许能解决。

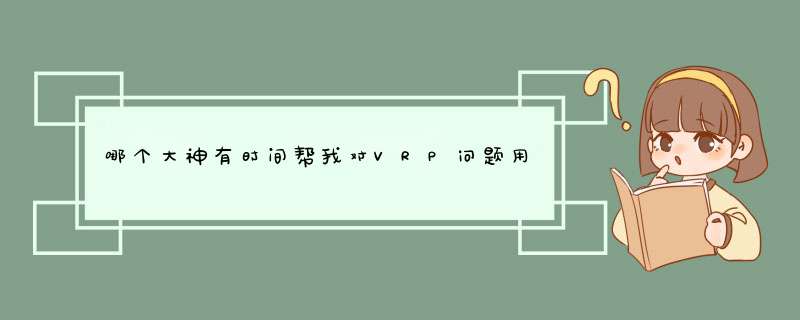
sets:

k/1..5/

z/1..8/:m

link(k,z):a,c,l,s

endsets

min=@sum(link:a)

@sum(z(j):a(4,j)*c(4,j))<=150

@sum(z(j):a(5,j)*c(5,j))<=400

@sum(z(j):a(1,j)*c(1,j))<=360+40*t

@sum(z(j):a(2,j)*c(2,j))<=600+30*t

@sum(z(j):a(3,j)*c(3,j))<=500+20*t

@for(z(j):@sum(k(i):a(i,j))=m(j))

t=@max(link(i,j):c(i,j)*(2*s(i,j)+2))

t<=10

data:

m=300 330 120 170 110 100 1000 700

s=3.08 2.5 2.6 5.74 4.28 6.2 2 3.86

1.16 3.14 4.12 5.06 2.36 5.52 1.96 2.96

4.48 6.64 6.74 2.9 3.28 1.86 3.34 2.04

4.8 4.5 5.4 8.1 8.2 6.55 5.74 4.32

1.84 2.58 3.92 3.74 3.84 3.98 3.82 2.36

enddata

---