红黑树---简单易懂

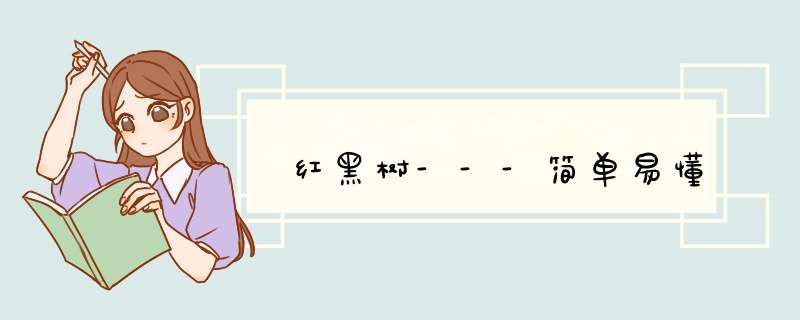
这样说呢，可能大家也猜到了是【二分查找法】，通过这个例子呢，主要想引出的是树，看下面的图片：

程序中的树呢，其实是我们日常看到的树的倒影，或者发挥一下想象，倒影也可以是树根

二叉查找树，Binary Search Tree 「BST」，要想了解二叉查找树呢，首先我们需要了解一下二叉查找树知耐斗都有哪些特性呢？

看个图就轻松理解上面三句话的意思了:

上图，结合二叉查找树的三条约束来看，非常好，没有什么问题。再来看一个图，依旧符合上面三条约束，感觉有问题吗？

这是一个走路一米六，一米八的树

这是一个畸形的树，大风一挂很可能被折断的树

从程序的角度来说这个树不够平衡，查找次数或时间复杂度 O(h)可能会随着一条腿长无限增长

理科生在高中学习生物时学过一个关键字「去除顶端优势」，通过去除植物顶端优势，侧芽会迅速生长，慢慢变得强壮和平衡， 红黑树其实就是去除二叉查找树顶端优势的解决方案，从而达到树的平衡

红黑树，Red-Black Tree 「RBT」是一个自平衡(不是绝对的平衡)的二叉查找树(BST)，树上的每个节点都遵循下面的规则:

可能大家还是很懵逼，不过没事，多练习几次就熟悉亩宏了。

红黑树有两大 *** 作：

我们会先尝试recolor，如果recolor不能达到红黑树的四个要求，然后我们尝试rotation，其实红黑树的关键玩法就是弄清楚recolor和rotation的规则，接下来我们看一下详细的算法公式吧。

假设我们插入的新节点为X

接下来看下图：

跟着上面的公式走：

上面说的是X的uncle为红色的情况，接下来我们看一下X的uncle为黑色的情况

当uncle节点为黑色的时候，我们第一步考虑的是旋转，这里呢我们可以先不关注红黑树的4个规则，主要是演示如何旋转的。

这种情况很简单，想象这是一根绳子，手提起P节点，然后变色即可，如下图：

变色：X是当前节点，P是X的parent节点，U是X的uncle节点，G是grand parent节点。P节点是根节点变黑色，G变成和X一样的颜色，也就是红色。完成

先进行左旋：使X的父节点P被X取代，同时父节点P成为X的左孩子，然后在应用 左左情况 ，如下图：

像左左一样，看成一根绳子。手提起P节点，然后变色即可，如下搭磨图：

先右旋：使 X 的父节点 P 被 X 取代，同时父节点 P 成为 X 的右孩子，然后再应用 右右情况 ，如下图：

通过上述过程，想必大家对红黑树有了一定的了解。以后在提到红黑树的时候，就不会那么头大了。本文参照 日拱一兵 公众号中的文章"红黑树，超强动静图详解，简单易懂".

参考文章

java8不是用红黑树来管顷皮仔理hashmap，而是在hash值相同的情况下（且重复数量大于握世8），用红黑树来管理数据。 红黑树相当于排序数据雀汪。可以自动的使用二分法进行定位。性能较高。

一般情况下，hash值做的比较好的话基本上用不到红黑树。

---