sin、 cos、 tan怎么算度数？

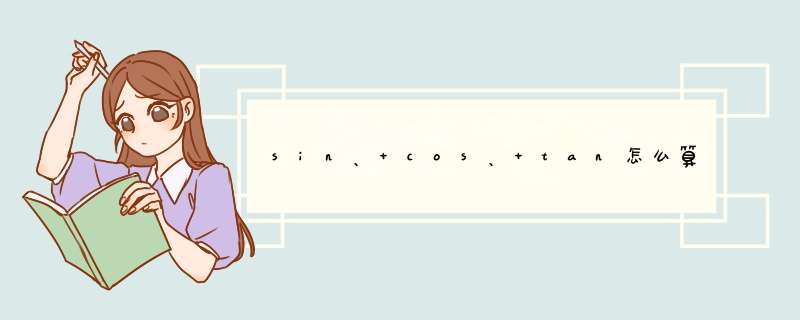
数学里用sin、cos、tan求度数要以靠以下公式：

一、sin度数公式

1、sin 30= 1/2

2、sin 45=根号2/2

3、sin 60= 根号3/2

二、cos度数公式

1、cos 30=根号3/2

2、cos 45=根号2/2

3、cos 60=1/2

三、tan度数公式

1、tan 30=根号3/3

2、tan 45=1

3、tan 60=根号3

扩展资料：

常见的三角函数包括正弦函数、余弦函数和正切函数。在航海学、测绘学、工程学等其他学科中，还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。

早期对于三角函数的研究可以追溯到古代。古希腊三角术的奠基人是公元前2世纪的喜帕恰斯。他按照古巴比伦人的做法，将圆周分为360等份（即圆周的弧度为360度，与现代的弧度制不同）。对于给定的弧度，他给出了对应的弦的长度数值，这个记法和现代的正弦函数是等价的。

已知正切的值如何手工求角度计算公式是怎样的
事实上,普通的计算器或电脑自带的计算器就能算了,也不能算是公式
k=tan a
a=arctan k
电脑自带的计算器 *** 作如下：
1选择 科学型 度
2输入k的大小
3点击Inv,原来的tan会变成tan-1,
4再点击这个tan-1就得到你要的角度了
如：
atand（1）=45

tan30°=√3/3（即：三分之一根三）。

tan45°=1。

tan60°=√3（即：根三）。

tan90°=∅（即：为无穷大）。

另外，常用的还有：

tan15°=2-√3（即：2-根3）。

tan75°=2+√3（即：2+根3）。

tan120°=-√3（即：负根三）。

tan135°=-1。

tan150°=-（√3/3）（即：负的三分之一根三）。

tan180°=0。

tan270°=∅（即：为无穷大）。

三角函数中，角A的正切值计算：tanA=∠A的对边/∠A的邻边。

扩展资料：

cot0°=∅（即：为无穷大）。

cot15°=2+√3（即：2+根3）

cot30°=√3（即：根三）。

cot45°=1。

cot60°=√3/3（即：三分之一根三）。

cot90°=0。

cot120°=-（√3/3）（即：负的三分之一根三）。

cot135°=-1。

cot150°=-√3（即：负根三）。

cot180°=∅（即：为无穷大）。

cot270°=0。

参考资料来源：百度百科——正切

                      百度百科——三角函数

可以利用反三角函数符号进行计算，以此版本计算器为

例：

1、打开此计算器，显示如下

2、以tan值为075为例，在此计算器中直接按tan-1键，再输入075，如图示

3、按下等于键便可得所求结果

扩展资料

反三角函数并不能狭义的理解为三角函数的反函数，是个多值函数。它是反正弦Arcsinx，反余弦Arccosx，反正切Arctanx，反余切Arccotx这些函数的统称，各自表示其正弦、余弦、正切、余切为x的角。

为限制反三角函数为单值函数，将反正弦函数的值y限在-π/2≤y≤π/2，将y作为反正弦函数的主值，记为y=arcsin x；相应地，反余弦函数y=arccos x的主值限在0≤y≤π；反正切函数y=arctan x的主值限在-π/2<y<π/2；反余切函数y=arccot x的主值限在0<y<π。

正切是tanα=b/a。

余切是cotα=a/b。

正弦是sinα=b/c。

余弦是cosα=a/c。

正割是secα=c/a。

余割是cscα=c/b。

正矢是versinθ=1-cosθ。

余矢是vercosθ=1-sinθ。

对于任意一个实数x，都对应着唯一的角（弧度制中等于这个实数），而这个角又对应着唯一确定的正切值tanx，按照这个对应法则建立的函数称为正切函数。

形式是f(x)=tanx　正切函数是区别于正弦函数的又一三角函数，它与正弦函数的最大区别是定义域的不连续性。

扩展资料

应用：

1、正切值在数值上与坡度相等，坡度=正切值x100%。

2、三角函数在复数领域有较为广泛的应用，在物理学方面也有一定的应用。

3、三角函数在勘测地形、勘探矿产方面发挥着重要的作用。

4、三角函数还用于通过视角来测量建筑物或山峰的高度。

常用正切值：tan225°=√2-1，tan30°=√3/3，tan45°=1，tan60°=√3，tan675°=√2+1，tan90°不存在。

参考资料来源：百度百科-正切值

tana=05，求a。a=arctan05≈26565度。

方法与步骤如下：

tana=05，a=arctan05

步骤1、用计算器数字键，输入05，如下图：

步骤2、点下图红框这个键，如下图：

步骤3、点下图红框这个键，如下图：

答案如下图的计算器显示数字：

扩展资料：

反正切函数（inverse
tangent）是数学术语，反三角函数之一，指函数y=tanx的反函数。计算方法：设两锐角分别为A，B，则有下列表示：若tanA=19/5，则
A=arctan19/5；若tanB=5/19，则B=arctan5/19。如果求具体的角度可以查表或使用计算机计算。

正切函数y=tanx在开区间（x∈(-π/2,π/2)）的反函数，记作y=arctanx 或 y=tan-1x，叫做反正切函数。它表示(-π/2,π/2)上正切值等于 x 的那个唯一确定的角，即tan(arctan x)=x，反正切函数的定义域为R即(-∞，+∞)。反正切函数是反三角函数的一种。

由于正切函数y=tanx在定义域R上不具有一一对应的关系，所以不存在反函数。注意这里选取是正切函数的一个单调区间。而由于正切函数在开区间(-π/2,π/2)中是单调连续的，因此，反正切函数是存在且唯一确定的。

引进多值函数概念后，就可以在正切函数的整个定义域(x∈R，且x≠kπ+π/2，k∈Z)上来考虑它的反函数，这时的反正切函数是多值的，记为
y=Arctan x，定义域是(-∞，+∞)，值域是 y∈R，y≠kπ+π/2，k∈Z。

于是，把 y=arctan x
(x∈(-∞，+∞)，y∈(-π/2,π/2))称为反正切函数的主值，而把 y=Arctan x=kπ+arctan x
(x∈R，y∈R，y≠kπ+π/2，k∈Z)称为反正切函数的通值。反正切函数在(-∞，+∞)上的图像可由区间(-π/2,π/2)上的正切曲线作关于直线
y=x 的对称变换而得到，。

反正切函数的大致图像如图所示，显然与函数y=tanx,（x∈R）关于直线y=x对称，且渐近线为y=π/2和y=-π/2。

参考资料来源：百度百科-反正切函数

---