向量a的模-向量b的模=向量a减向量b的模 求向量a与向量a加向量b的夹角

|a|-|b|=|a-b|,
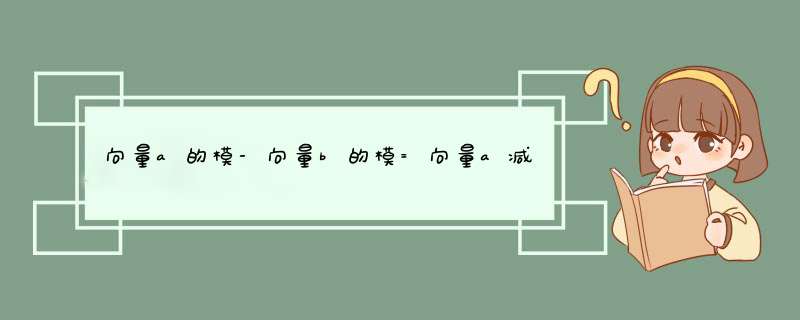
平方得a^2-2|a||b|+b^2=a^2-2ab+b^2,
∴ab=|a||b|,
∴向量a与b同向，
∴向量a与向量a加向量b的夹角是0°。

|a|-|b|=|a-b|
即：|a|^2+|b|^2-2|a||b|=|a|^2+|b|^2-2a·b
即：2|a||b|=2|a||b|cos<a,b>
如果：a和b均为非零向量，则：cos<a,b>=1
即：<a,b>=0，即a和b同向
但如果a和b其中一个为零向量，则<a,b>是任意的
但零向量的方向是任意的，也可以认为与另一个非零向量方向相同
但a和b都是零向量时，就不对了

向量a+向量b的模

=|向量a+向量b|

=根号下（向量a+向量b）²

=根号下（|a|²+|b|²+2|a||b|cosα）

cosα是向量a和向量b的夹角

扩展资料：

在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的只有大小，没有方向的量叫做数量（物理学中称标量）。

向量  的大小，也就是向量  的长度（或称模），记作  。

向量的性质

向量的模的运算没有专门的法则，一般都是通过余弦定理计算两个向量的和、差的模。

多个向量的合成用正交分解法，如果要求模一般需要先算出合成后的向量。

模是绝对值在二维和三维空间的推广，可以认为就是向量的长度。推广到高维空间中称为范数。

空间向量(x,y,z)，其中x,y,z分别是三轴上的坐标，模长是：

平面向量（x，y），模长是：

参考资料：

百度百科-向量的模

---