除法是如何计算的？

有一点，你说的很对，乘法是除法的逆运算。计算除法的时候，可以用乘法算。如，计算24除以3，可以这样想，3乘几等于24，商就是几。因为3乘8等于24，所以，24除以3等于8。
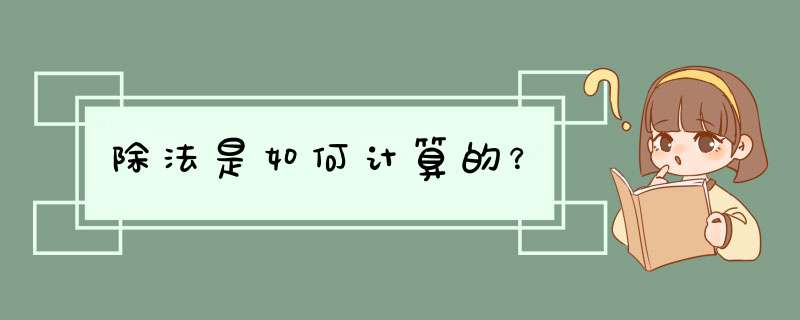
再如3除以5，可以想5乘几等于5，因为5乘06等于5，所以3除以5等于06。
当然，对于比较复杂的除法，还是应该学会用竖式计算。

第1步骤：观察规律。

观察 除法的简便运算方法 ,具有普遍性，以实例讲解。用168和4为例。

第2步骤：画出除数运算符"√"

运算符 "√" 表示正在进行的运算是竖式除法。

第3步骤：确定对应位置。

把被除数写在竖式除号里面，竖式写在竖式除号外面。

第4步骤：确定对应位置。

商写在竖式除号上面，记得对齐被除数的个位哦!

第5步骤：确定积。

商写在竖式除号上面，记得对齐被除数的个位哦!

第6步骤：计算结果。

整个运算过程如下，要细心做题!

168 ÷ 4 = 420

☞ 欢迎来到神奇的01世界 ☜

顾名思义，纳皮尔筹就是一个叫纳皮尔的人发明的算筹。

纳皮尔作为苏格兰著名的数学家并没有太过著名，想必大多数人都闻所未闻，然而他发明的一个数学概念却是每个高中生都会掌握的、大名鼎鼎的对数。看来纳皮尔没有把对数命名为纳皮尔数，这波真是亏大了。

纳皮尔出生于一个地主家庭，但他没有按照惯例成为一个傻儿子。他的父亲不仅是地主、官员，还是苏格兰造币厂的老大，16岁就……少来得子；他的母亲也是个门当户对的官二代；后来这个丧心病狂的家族还专门用自己的姓氏创立了一个爵位——纳皮尔勋爵，这波不亏了……

作为一个贵族，纳皮尔自小接受家庭私教，没上小学，到了13岁……就被送去了圣安德鲁斯大学；大学没上多久又辍学跑到欧洲大陆进修，但没人知道他在21岁回来前都进修了些啥（是的21岁就完成了大学之后的进修）；24岁买了座城堡住了几十年，58岁父亲死后又搬到了父亲的城堡里去，一直住到67岁去世。除了显赫的家世，纳皮尔自身的生平实在没有留下多少令人津津乐道的故事。

他就像卯足了一生的劲，要为数学界做出一些贡献，靠生命中的最后三年名垂青史。

1614年，64岁的纳皮尔出版了《奇妙的对数表的描述》一书，成为人类从上帝手中取得对数的标志。后人把书中提到的一种特殊对数称为 纳皮尔对数 ：

PS：第一次用Markdown写公式，真好。希望不会吓跑跟我一样害怕数学的读者……

有了对数，乘除就能化简为加减，大大减轻了当时科学界的计算量。

无独有偶，纳皮尔筹的发明同样也是为了将乘除等复杂运算降解为加减。

1617年，介绍纳皮尔筹的专著《Rabdologiæ》 [1] 在爱丁堡出版，67岁的老纳皮尔潇洒辞世，留给世人对数之外的第二件珍贵遗产。

纳皮尔筹材质多样，木质、金属、硬纸板，英文叫做Napier's Bones，也许最早用的是兽骨（可不是纳皮尔的骨头啊），因此也常称 纳皮尔骨筹 ；由于形状是一根根的小棒，也常称 纳皮尔棒 。

虽是筹算，纳皮尔筹却用到了一个「算盘」，在计算时盛放算筹。算盘的左边框从上至下标注着 1~9 ，与每根算筹上的9个方格一一对应。算筹有10种，筹上的方格里分别填着 0~9 与左边框数字的乘积，简单地说，这是一张九九乘法表。

除了顶部的第一个方格，下面的8个方格都划有对角线，将十位数与个位数分开，这么做是为了使用了一种叫做格子乘法（或更形象地称之为百叶窗乘法）的算法。举个例子：

取用被乘数6、7、8、5四根筹，而后把目光投到第8行上：

以斜线为界，对每一位进行相加，超过9时通过心算进行进位：

这是最简单的乘法，除法的步骤稍微复杂一些，开方运算则更加繁复，还需要引入一种专用的新筹，具体算法在此展开的意义不大，感兴趣的朋友可自行移步 维基娘 。

《Rabdologiæ》被译成多种文字（包括中文），纳皮尔筹风靡一时，后来出现了许多改进和变种，比如把筹做成可以旋转的圆柱：

此类圆柱形纳皮尔筹给后来机械式计算器的问题提供了灵感，以德国的威廉·契克卡德（Wilhelm Schickard）、意大利的蒂托·布拉蒂尼（Tito Burattini）、英国的塞缪尔·莫兰（Samuel Morland）、法国的勒内·格里耶（René Grillet）为代表的一众机械计算先驱都以纳皮尔筹为基础构建了机械式计算器。

到了19世纪，为了便于读数，干脆把纳皮尔筹做成了斜的：

1628年传入中国后，也出现了各式各样的本土化变形，比如清代数学家梅文鼎把它改成了以半圆代替对角线的横筹：

除法运算公式：

1、被除数÷除数=商，例如：8÷4=2。

2、被除数÷商=除数，例如：8÷4=2→8÷2=4。

3、除数×商=被除数，例如：2×4=8。

4、带有余数的情况：

被除数÷除数=商余数（其中，余数小于除数）⇋除数×商+余数=被除数。

扩展资料：

根据除法的意义，除法是已知两个因数的积与其中一个因数，求另一个因数的运算。利用除法与乘法的互逆关系可知，如果除数为0，则：

1、当被除数不为0（例如3÷0），由于“任何数乘0都等于0，而不可能等于不是0的数（例如3）”，此时除法算式的商不存在——即任何数的0倍都不可能为非零数；

2、当被除数为0，即除法算式0÷0，由于“任何数乘0都等于0”，于是商可以是任何数——即任何数的0倍都等于0。

为了避免以上两种情况，数学中规定“0不能做除数”。

---