在1--100这100个自然数中,至少选几个数,才能保证取出的数中,有俩个数的差是50

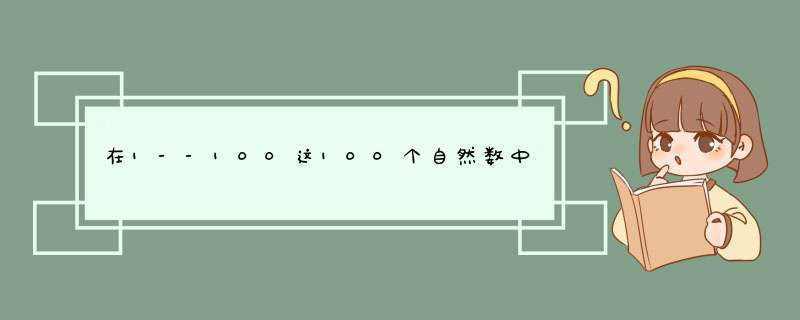
51个。1-100中共有49对数满足条件：1和99，2和98，49和51由抽屉原理可知，当我们选完1-50之后，任意选一个数都能满足条件，也就是51。

乘法，是指将相同的数加起来的快捷方式。其运算结果称为积，“x”是乘号。从哲学角度解析，乘法是加法的量变导致的质变结果。整数（包括负数），有理数（分数）和实数的乘法由这个基本定义的系统泛化来定义。

乘法也可以被视为计算排列在矩形（整数）中的对象或查找其边长度给定的矩形的区域。 矩形的区域不取决于首先测量哪一侧，这说明了交换属性。 两种测量的产物是一种新型的测量，例如，将矩形的两边的长度相乘给出其面积，这是尺寸分析的主题。

#include <stdioh>

#include <stdlibh>

#include <timeh>

int main()

{

    int a[50],sum,cnt,i;

    srand(time(NULL));

    for(i=0,cnt=0;i<50;++i)

    {

        a[i]=rand()%100+1;

        if(a[i]%2)

        {

            sum+=a[i];

            cnt++;

        }

        printf("%3d%c",a[i],(i+1)%10' ':'\n');

    }

    printf("%d %f",cnt,(float)sum/cnt);

    return 0;

}

权当两表分别为sheet1、sheet2，姓名均在A列
在1表的B1粘贴以下公式
=IF(COUNTIF(sheet1!A:A,A1),"Yes","")
下拉
即可标记出来

恰有50次品：C(800,50)C(200,50)/C(1000,100)

没有次品：C(800,100)/C(1000,100)

1个次品：C(800,99)C(200,1)/C(1000,100)

2个次品：C(800,98)C(200,2)/C(1000,100)

3个次品：C(800,97)C(200,3)/C(1000,100)

最多3个次品：C(800,100)/C(1000,100)+C(800,99)C(200,1)/C(1000,100)+C(800,98)C(200,2)/C(1000,100)+C(800,97)C(200,3)/C(1000,100)

至少3个次品：1-C(800,100)/C(1000,100)-C(800,99)C(200,1)/C(1000,100)-C(800,98)C(200,2)/C(1000,100)

可以使用vlookup函数。函数具体运用如下：

1、在表1中 姓名信息后任意插入一列，引用公式vlookup。

2、因为是根据姓名调用数据，可以在“lookup-value”（表示要查找的属性值）栏单击姓名所在单元格。

3、在“table-array”选择表2中想要调用的信息，假设想要调用B11“”的信息。

4、因为B11所在的列为 第11列，所以在 col-index-num里面输入11，在range-lookup输入0，亦可以不输入。不输入状态下默认错误返回乱码。

什么是抽屉原理，这个我只能大致说下吧。很简单，就是3个抽屉，放4个苹果，必有2个苹果在同一个抽屉里。哈哈，这道题我是这样想的。
1到100，可以看成50个奇数和50个偶数。每次取一个数，则必然是奇数或者偶数。如果在51次取数过程中，出现了2次或者2次以上，取到偶数了，则其中一定至少有2个数（就是取到的偶数），他们中的某一个是另一个的整数倍。这个可以理解吧。
因此，如果51次中只取到1个偶数，那就是说，剩下的50个奇数，全部被取到，那更简单，3和9肯定被取到，而9是3的3倍。
而51次取数，偶数至少被取到1次（因为奇数只有50个），这就是利用抽屉原理，可以得到结论：从数集1，2，3，……99，100中任意选取51个数，其中一定有2个数，他们中的某一个是另一个的整数倍

---