如何编写求图像的熵的Matlab程序

求图像的熵，在许多场合下都有应用，也可以有多种编写程序的方法，下面介绍作者编写的一个图像熵的函数yentropy()，可以直接调用。可以用于求图像的局部熵，也可以求其整体熵。

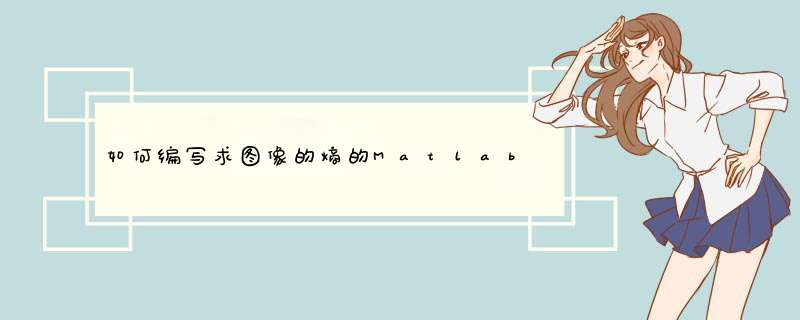
function entr=yentropy(a)

a=uint8(a) %这里a为8位的单色图像或24为的RGB彩色图像

[m n l]=size(a)

entr=0

for k=1:l

hi=zeros(1,256)

for i=1:m

for j=1:n

hi(a(i,j,k)+1)=hi(a(i,j,k)+1)+1 %求每种值的在图像中出现的次数

end

end

hi=sort(hi,'descend')

hi=hi./m./n %求概率

en=0.0

for i=1:256

if hi(i)>0

en=en-hi(i).*log2(hi(i)) %概率不为0 累加求熵

else

i=257 %否则停止

end

end

entr=entr+en

end

entr=entr/l %当l=1时a为单色图像；当l=3时a为彩色图像，三个页面的熵平均

1、熵是描述区域的随机程度的，P=ΣC*logC，C是灰度概率值，当图像均匀时，各灰度值的概率基本相等，熵可以达到最大

2、例程：

#include<iostream.h>

#include<math.h>

int i,j

double rowsum(double table[][4],int nrow)//定义第i行的边际概率函数

{

for(i=0i<nrowi++)

{

   for( j=1j<4j++)

    table[i][0]+=table[i][j] 

}

return 0

}

double liesum(double table[4][4],int nlie)//定义第j列的边际概率函数

{ for( j=0j<nliej++)

{

   for( i=1i<4i++)

    table[0][j]+=table[i][j]

}

    return 0

}

void main()

{ 

double p[4][4]={{1.0/8.0,1.0/16.0,1.0/32.0,1.0/32.0},{1.0/16.0,1.0/8.0,1.0/32.0,1.0/32.0},

{1.0/16.0,1.0/16.0,1.0/16.0,1.0/16.0},{1.0/4.0,0.0,0.0,0.0}}

for ( i=0i<4i++)//输出概率矩阵

{

   for ( j=0j<4j++)

    cout<<p[i][j]<<" "

      cout<<endl      

}cout<<endl 

rowsum(p,4)//调用函数输出第i行的边际概率 

for (i =0i<4i++)

{cout<<"第"<<i<<"行的边际概率p"<<"["<<i<<"]"<<"是"<<p[i][0]<<endl}cout<<endl

liesum(p,4)//调用函数输出第j列的边际概率

for ( j =0j<4j++)

{cout<<"第"<<j<<"列的条件概率p"<<"["<<j<<"]"<<"是"<<p[0][j]<<endl}cout<<endl

// double p[4][4]

double H1=0.0

for( i=0i<4i++)

{H1+=p[i][0]*(log((1.0/p[i][0])/log(2.0)))}

    double H2=0.0

for( j=0j<4j++)

{H2+=p[0][j]*(log((1.0/p[0][j])/log(2.0)))}

    double H3=0.0 

for(i=0i<3i++)

for(j=0j<4j++) 

{H3+=p[i][j]*(log(1.0/p[i][j])/log(2.0))}

H3+=p[4][1]*(log(1.0/p[4][1])/log(2.0))

    cout<<"X的熵：H(X)="<<H1<<endl

cout<<"Y的熵：H(Y)="<<H2<<endl

    cout<<"(X,Y)的熵：H(X,Y)="<<H3<<endl

cout<<endl

cout<<"条件熵：H(X|Y)="<<H3-H2<<endl

cout<<"条件熵：H(Y|X)="<<H3-H1<<endl

cout<<"互信息：I(XY)="<<H1+H2-H3<<endl

int size=4//定义联合概率p为维数组

double *p

p=new double[size] 

for ( i=0i<4i++)//联合概率计算

{

   for ( j=0j<4j++)

   {

      /*int nSize 

            scanf( "%d", &nSize ) 

            int *p = ( int* )malloc( sizeof( int ) * nSize ) 

            for( int i = 0 i < nSize i++ ) 

            p[ i ] = 0

            

    double table[4][4]

        p[i]=pp[0][i]*table[i][j]

    cout<<"联合概率"<<"p"<<"["<<i<<"]"<<"["<<j<<"]""是"<<p[i]<<endl

   

   }

}

for ( i=0i<4i++)//联合熵的计算

{

   for ( j=0j<4j++)

   {   

   

   // H+=p[i][j]*log(1.0/p[i][j])

    H+=p[i]*(log((1.0/p[i])/log(2.0)))

   }

}

cout<<"联合H(x,y)熵为"<<H<<endl

delete []p */

}

%计算一副图像的熵

%随机生成图像

A=floor(rand(8,8).*255)

[M,N]=size(A)

temp=zeros(1,256)

%对图像的灰度值在[0,255]上做统计

for

m=1:M

for

n=1:N

if

A(m,n)==0

i=1

else

i=A(m,n)

end

temp(i)=temp(i)+1

end

end

temp=temp./(M*N)

%由熵的定义做计算

result=0

for

i=1:length(temp)

if

temp(i)==0

result=result

else

result=result-temp(i)*log2(temp(i))

end

end

result

%计算联合熵

%随机生成图像

A=floor(rand(8,8).*255)

B=floor(rand(8,8).*255)

[M,N]=size(A)

temp=zeros(256,256)

%对图像的灰度值成对地做统计

for

m=1:M

for

n=1:N

if

A(m,n)==0

i=1

else

i=A(m,n)

end

if

B(m,n)==0

j=1

else

j=B(m,n)

end

temp(i,j)=temp(i,j)+1

end

end

temp=temp./(M*N)

%由熵的定义做计算

result=0

for

i=1:size(temp,1)

for

j=1:size(temp,2)

if

temp(i,j)==0

result=result

else

result=result-temp(i,j)*log2(temp(i,j))

end

end

end

result

---