SDUTOJ 3664 - 顺序表应用7：最大子段和之分治递归法

SDUTOJ 3664 - 顺序表应用7：最大子段和之分治递归法

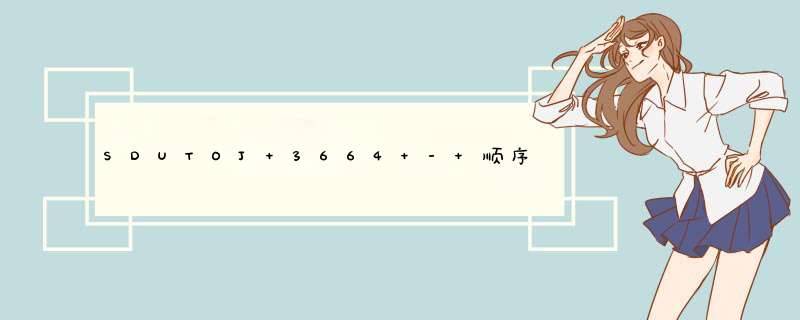
#include
using namespace std;

int a[50010] = {0};
int count_num = 0; // 记录递归次数
int sum = 0;

int maxSub(int l, int r)
{
    count_num++; // 统计递归次数
    if (l == r){ // 递归出口
        if (a[l] > 0){
            sum = a[l];
        }
        else{ // 负串记0
            sum = 0;
        }
    }
    else{
        int mid = (l+r)/2;
        int l_res = maxSub(l, mid); // 左半部分最大子串
        int r_res = maxSub(mid+1, r); // 右半部分最大子串
        int s = 0;
        // 横跨左右的最大子串
        for (int i = l; i <= r; i++){
            if (s+a[i] > 0){ // 正串更新
                sum = max(sum, s=s+a[i]);
            }
            else{ // 负串记0
                s = 0;
            }
        }
        // 更新sum为最大子串长度
        sum = max(sum, l_res);
        sum = max(sum, r_res);
    }
    return sum;
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++){
        scanf("%d", &a[i]);
    }
    int res = maxSub(0, n-1);
    printf("%d %dn", res, count_num);
    return 0;
}