Python实现t-SNE+DBSCAN+GASVR的组合预测模型

Python实现t-SNE+DBSCAN+GASVR的组合预测模型

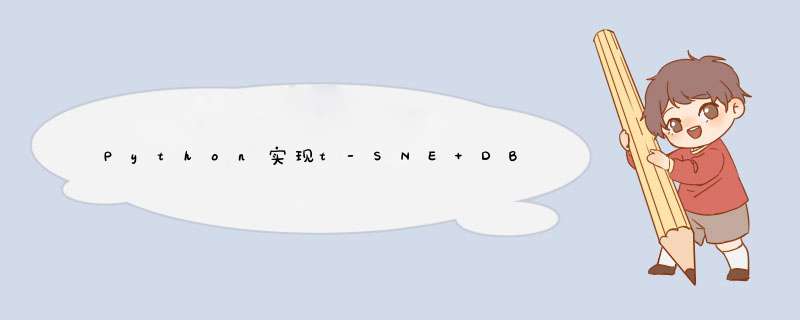
本模型的思路为使用t-SNE降维，使用DBSCAN降噪，GASVR进行预测。

在一定程度上具有参考价值，但因除噪时并未填补会导致数据中断，故在时间序列预测上并不具有实际实用价值，需要进行数据填补。且本模型只强调模型的精度，并不考虑数据之间的关联性，故原数据集将被打散。

1.引入数据

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import explained_variance_score
from sklearn.ensemble import RandomForestRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN

import numpy as np
import time

from sklearn import metrics

import csv

data=[]
traffic_feature=[]
traffic_target=[]
csv_file = csv.reader(open('dongyinghaishui(10m)1.csv'))
for content in csv_file:
    content=list(map(float,content))
    if len(content)!=0:
        data.append(content)
        traffic_feature.append(content[0:4])
        traffic_target.append(content[-1])
#print('data=',data)
#print('traffic_feature=',traffic_feature)
#print('traffic_target=',traffic_target)
data=np.array(data)
traffic_feature=np.array(traffic_feature)
traffic_target=np.array(traffic_target)
data.shape

数据格式：(3977, 5)

2.标准化

scaler = StandardScaler() # 标准化转换
scaler.fit(traffic_feature)  # 训练标准化对象
traffic_feature= scaler.transform(traffic_feature)   # 转换数据集
feature_train, feature_test, target_train, target_test = train_test_split(traffic_feature, traffic_target, test_size=0.05,random_state=17)

3.测试单SVR效果

from sklearn.svm import SVR
import matplotlib.pyplot as plt  
start1=time.time()
model_svr = SVR(C=1,epsilon=0.1,gamma=10)
model_svr.fit(feature_train,target_train)
predict_results1=model_svr.predict(feature_test)
end1=time.time()

SVRRESULT=predict_results1

plt.plot(target_test)#测试数组
plt.plot(predict_results1)#测试数组
plt.legend(['True','SVR'])
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.title("SVR")  # 标题
plt.show()
print("EVS:",explained_variance_score(target_test,predict_results1))
print("R2:",metrics.r2_score(target_test,predict_results1))
print("Time:",end1-start1)

EVS: 0.4797244273713823
R2: 0.46414774637696155
Time: 0.529613733291626

4.使用PCA确定降维价数

from sklearn.decomposition import PCA
pca = PCA(n_components=4)
newX = pca.fit_transform(traffic_feature)
print(np.around(pca.explained_variance_ratio_, 3))

x_data = ['1','2','3','4']
y_data = np.around(pca.explained_variance_ratio_, 3)
# 绘图
plt.bar(x=x_data, height=y_data,color='steelblue', alpha=0.8)
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.title("Contribution rate of each principal component")
# 为两条坐标轴设置名称
plt.xlabel("Principal Component")
plt.ylabel("Contribution rate of each principal component/%")
print(np.around(pca.explained_variance_ratio_, 3))

[0.467 0.251 0.181 0.101]

4价比重已占90%以上，故降维至4价即可。

5.t-SNE三维压缩

from sklearn.manifold import TSNE
newData = TSNE(n_components=3,random_state=17).fit_transform(newX)
plt.scatter(newData[:, 0],newData[:, 1],newData[:, 2])
plt.title("PCA-TSNE")  # 标题
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.show()

6.分别引入kmeans和DBSCAN做降噪对比

#Kmeans
t0 = time.time()
kmeans = KMeans(init = 'k-means++',n_clusters=10, random_state=10).fit(newData)
t = time.time() - t0
plt.scatter(newData[:, 0], newData[:, 1],newData[:, 2],c=kmeans.labels_)
plt.title('Kmeans time : %f'%t)
fig = plt.gcf()


fig.set_size_inches(18.5, 10.5)
plt.show()

 

 看得出，并不能很好的识别出噪音点。

#DBSCAN
t0 = time.time()
dbscan = DBSCAN(eps=0.1,min_samples=2).fit(newData)
t = time.time()-t0
plt.scatter(newData[:, 0], newData[:, 1],newData[:, 2],c=dbscan.labels_)
plt.title('DBSCAN time: %f'%t)
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.show()

 孤立的噪音较多。

7.使用DBSCAN降噪

#DBSCAN 降噪后

dbscan = DBSCAN(eps=0.1,min_samples=2).fit(newData)

YYY=[]
XXX=[]
C=[]
for inx,i in enumerate(dbscan.labels_):
    if i==-1:
        YYY.append(i)
        XXX.append(newData[inx])
        C.append(inx)
        
XXX=np.array(XXX)
XXX=XXX.astype(np.float64)
plt.scatter(XXX[:, 0], XXX[:, 1], XXX[:, 2],c=YYY)
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.title('DBSCAN After noise reduction time: %f'%t)
plt.show()

降噪后的效果

8 .进行数据还原

XXX
CCC=[]
DDD=[]
a=1

for inx,i in enumerate(traffic_target):
    for j in C:
        if(inx==j):
            a=1+a
            CCC.append(i)
            DDD.append([a,i])
        

CCC=np.array(CCC)
DDD=np.array(DDD)

DDD.shape
dbscan = DBSCAN(eps=1,min_samples=5).fit(DDD)
plt.scatter(DDD[:,0],DDD[:,1],c=dbscan.labels_)
plt.title('DBSCAN')
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.show()

还原后的数据

 9.将还原的数据进行SVR预测

after_feature_train,after_feature_test,after_target_train, after_target_test = train_test_split(XXX,CCC,test_size=0.05,random_state=17)
start=time.time()
model_svr = SVR(C=1,epsilon=0.1,gamma=10)
model_svr.fit(XXX,CCC)
after_predict_result=model_svr.predict(after_feature_test)
end=time.time()

DBSCANSVRRESULT=after_predict_result
plt.plot(after_predict_result)#测试数组
plt.plot(after_target_test)#测试数组
plt.title("DBSCAN-SVR")  # 标题
plt.legend(['True','DBSCAN-SVR'])
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.show()
print("EVS:",explained_variance_score(after_target_test,after_predict_result))
print("R2:",metrics.r2_score(after_target_test,after_predict_result))
print("Time:",end-start)

效果如下

EVS: 0.8250398436521921
R2: 0.8018421163998288
Time: 0.26456522941589355

明显有了极大的提升，但还不够。

10.引入GA

XXX = XXX.tolist()
CCC = CCC.tolist()
RRR=after_feature_test.tolist()
LLL=after_target_test.tolist()
def msefunc(predictval,realval):
   # squaredError = []
    #absError = []
    #for i in range(len(predictval)):
     #   val=predictval[i-1]-realval[i-1]
      #  squaredError.append(val * val)  # target-prediction之差平方 

    print("R2 = ",metrics.r2_score(realval,predictval)) # R2
    return metrics.r2_score(realval,predictval)
 
def SVMResult(vardim, x, bound):
    X = XXX
    y = CCC
    c=x[0]
    e=x[1]
    g=x[2]
    clf = SVR(C=c,epsilon=e,gamma=g)

    clf.fit(X, y)
    predictval=clf.predict(RRR)
    return msefunc(predictval,LLL)
 class GAIndividual:
 
    '''
    individual of genetic algorithm
    '''
 
    def __init__(self,  vardim, bound):
        '''
        vardim: dimension of variables
        bound: boundaries of variables
        '''
        self.vardim = vardim
        self.bound = bound
        self.fitness = 0.
 
    def generate(self):
        '''
        generate a random chromsome for genetic algorithm
        '''
        len = self.vardim
        rnd = np.random.random(size=len)
        self.chrom = np.zeros(len)
        for i in range(0, len):
            self.chrom[i] = self.bound[0, i] + 
                (self.bound[1, i] - self.bound[0, i]) * rnd[i]
 
    def calculateFitness(self):
        '''
        calculate the fitness of the chromsome
        '''
        self.fitness = SVMResult(self.vardim, self.chrom, self.bound)
import random
import copy

 
class GeneticAlgorithm:
 
    '''
    The class for genetic algorithm
    '''
 
    def __init__(self, sizepop, vardim, bound, MAXGEN, params):
        '''
        sizepop: population sizepop人口规模
        vardim: dimension of variables变量维数
        bound: boundaries of variables变量边界
        MAXGEN: termination condition终止条件
        param: algorithm required parameters, it is a list which is consisting of crossover rate, mutation rate, alpha
        '''
        self.sizepop = sizepop
        self.MAXGEN = MAXGEN
        self.vardim = vardim
        self.bound = bound
        self.population = []
        self.fitness = np.zeros((self.sizepop, 1))
        self.trace = np.zeros((self.MAXGEN, 3))
        self.params = params
 
    def initialize(self):
        '''
        initialize the population
        '''
        for i in range(0, self.sizepop):
            ind = GAIndividual(self.vardim, self.bound)
            ind.generate()
            self.population.append(ind)
 
    def evaluate(self):
        '''
        evaluation of the population fitnesses
        '''
        for i in range(0, self.sizepop):
            self.population[i].calculateFitness()
            self.fitness[i] = self.population[i].fitness
 
    def solve(self):
        '''
        evolution process of genetic algorithm
        '''
        self.t = 0
        self.initialize()
        self.evaluate()
        best = np.max(self.fitness)
        bestIndex = np.argmax(self.fitness)
        self.best = copy.deepcopy(self.population[bestIndex])
        self.avefitness = np.mean(self.fitness)
        self.maxfitness = np.max(self.fitness)
        
        self.trace[self.t, 0] =  self.best.fitness
        self.trace[self.t, 1] =  self.avefitness
        self.trace[self.t, 2] =  self.maxfitness
        print("Generation %d: optimal function value is: %f; average function value is %f;max function value is %f"% (
            self.t, self.trace[self.t, 0], self.trace[self.t, 1],self.trace[self.t, 2]))
        while (self.t < self.MAXGEN - 1):
            self.t += 1
            self.selectionOperation()
            self.crossoverOperation()
            self.mutationOperation()
            self.evaluate()
            best = np.max(self.fitness)
            bestIndex = np.argmax(self.fitness)
            if best > self.best.fitness:
                self.best = copy.deepcopy(self.population[bestIndex])
            self.avefitness = np.mean(self.fitness)
            self.maxfitness = np.max(self.fitness)
            
            self.trace[self.t, 0] =  self.best.fitness
            self.trace[self.t, 1] = self.avefitness
            self.trace[self.t, 2] =  self.maxfitness
            print("Generation %d: optimal function value is: %f; average function value is %f;max function value is %f"% (
            self.t, self.trace[self.t, 0], self.trace[self.t, 1],self.trace[self.t, 2]))
 
        print("Optimal function value is: %f; " %
              self.trace[self.t, 0])
        print ("Optimal solution is:")
        print (self.best.chrom)
        self.printResult()
 
    def selectionOperation(self):
        '''
        selection operation for Genetic Algorithm
        '''
        newpop = []
        totalFitness = np.sum(self.fitness)
        accuFitness = np.zeros((self.sizepop, 1))
 
        sum1 = 0.
        for i in range(0, self.sizepop):
            accuFitness[i] = sum1 + self.fitness[i] / totalFitness
            sum1 = accuFitness[i]
 
        for i in range(0, self.sizepop):
            r = random.random()
            idx = 0
            for j in range(0, self.sizepop - 1):
                if j == 0 and r < accuFitness[j]:
                    idx = 0
                    break
                elif r >= accuFitness[j] and r < accuFitness[j + 1]:
                    idx = j + 1
                    break
            newpop.append(self.population[idx])
        self.population = newpop
 
    def crossoverOperation(self):
        '''
        crossover operation for genetic algorithm
        '''
        newpop = []
        for i in range(0, self.sizepop, 2):
            idx1 = random.randint(0, self.sizepop - 1)
            idx2 = random.randint(0, self.sizepop - 1)
            while idx2 == idx1:
                idx2 = random.randint(0, self.sizepop - 1)
            newpop.append(copy.deepcopy(self.population[idx1]))
            newpop.append(copy.deepcopy(self.population[idx2]))
            r = random.random()
            if r < self.params[0]:
                crossPos = random.randint(1, self.vardim - 1)
                for j in range(crossPos, self.vardim):
                    newpop[i].chrom[j] = newpop[i].chrom[
                        j] * self.params[2] + (1 - self.params[2]) * newpop[i + 1].chrom[j]
                    newpop[i + 1].chrom[j] = newpop[i + 1].chrom[j] * self.params[2] + 
                        (1 - self.params[2]) * newpop[i].chrom[j]
        self.population = newpop
 
    def mutationOperation(self):
        '''
        mutation operation for genetic algorithm
        '''
        newpop = []
        for i in range(0, self.sizepop):
            newpop.append(copy.deepcopy(self.population[i]))
            r = random.random()
            if r < self.params[1]:
                mutatePos = random.randint(0, self.vardim - 1)
                theta = random.random()
                if theta > 0.5:
                    newpop[i].chrom[mutatePos] = newpop[i].chrom[
                        mutatePos] - (newpop[i].chrom[mutatePos] - self.bound[0, mutatePos]) * (1 - random.random() ** (1 - self.t / self.MAXGEN))
                else:
                    newpop[i].chrom[mutatePos] = newpop[i].chrom[
                        mutatePos] + (self.bound[1, mutatePos] - newpop[i].chrom[mutatePos]) * (1 - random.random() ** (1 - self.t / self.MAXGEN))
        self.population = newpop
 
    def printResult(self):
        '''
        plot the result of the genetic algorithm
        '''
        x = np.arange(0, self.MAXGEN)
        y1 = self.trace[:, 0]
        y2 = self.trace[:, 1]
        y3 = self.trace[:, 2]
        #plt.plot(x, y1, 'r', label='optimal value')
        plt.plot(x, y2, 'g', label='average value')
        plt.plot(x, y3, 'b', label='max value')
        fig = plt.gcf()
        fig.set_size_inches(18.5, 10.5)
        plt.xlabel("GENS")
        plt.ylabel("R2")
        plt.title("GA")
        plt.legend()
        plt.show()

if __name__ == "__main__":
 
   bound = np.array([[0,0,0],[10,2,100]])
    
   ga = GeneticAlgorithm(20, 3, bound, 20, [0.9, 0.1, 0.5])
   ga.solve()

11.将优化后的参数代入SVR

after_feature_train,after_feature_test,after_target_train, after_target_test = train_test_split(XXX,CCC,test_size=0.05,random_state=17)
svr = SVR(C=3.9505118,epsilon=0.15014702,gamma=38.02146648)
start=time.time()
svr.fit(XXX,CCC)
after_predict_result=svr.predict(after_feature_test)
end=time.time()
DBSCANSVRGARESULT=[]
DBSCANSVRGARESULT=after_predict_result
plt.plot(after_predict_result,marker='o')#测试数组
plt.plot(after_target_test,marker='x')

plt.title("DBSCAN-SVR-GA")  # 标题
plt.legend(['True','DBSCAN-SVR-GA'])
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.show()
print("EVS:",explained_variance_score(after_target_test,after_predict_result))
print("R2:",metrics.r2_score(after_target_test,after_predict_result))
print("Time:",end-start)

 

EVS: 0.9919232390408123
R2: 0.9919208479231462
Time: 0.32965993881225586

已经不能再好了吧...

12.只用GASVR做对比

调优过程略...

start1=time.time()
model_svr =SVR(C=3.9505118,epsilon=0.15014702,gamma=38.02146648)
model_svr.fit(feature_train,target_train)
predict_results1=model_svr.predict(feature_test)
SVRGARESULT=[]
SVRGARESULT=predict_results1
end1=time.time()
plt.plot(target_test)#测试数组
plt.plot(predict_results1)#测试数组
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.title("SVR-GA")  # 标题
plt.legend(['True','SVR-GA'])
plt.show()
print("EVS:",explained_variance_score(target_test,predict_results1))
print("R2:",metrics.r2_score(target_test,predict_results1))
print("Time:",end1-start1)

EVS: 0.6045876080406886
R2: 0.5994740318045189
Time: 0.8312788009643555

差的远呢...

13.做个BPNN为对比

YY=[]
for i in CCC:
    YY.append([i])
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()

x=XXX
y=YY
x_t=np.array(x)
y_true=np.array(y)
mm=MinMaxScaler() #实例化
std=mm.fit(x_t) #训练模型
x_true=std.transform(x_t) #转化
print(x_true)
print(y_true)
X=tf.placeholder(tf.float32,[None,3])
Y=tf.placeholder(tf.float32,[None,1])

w1=tf.Variable(tf.truncated_normal([3,3],stddev=0.001))
b1=tf.Variable(tf.zeros([3]))
w2=tf.Variable(tf.zeros([3,1]))
b2=tf.Variable(tf.zeros([1]))
L1=tf.nn.relu(tf.matmul(X,w1)+b1)
y_pre=tf.matmul(L1,w2)+b2
loss=tf.reduce_mean(tf.cast(tf.square(Y-y_pre),tf.float32))
train_op=tf.train.GradientDescentOptimizer(0.1).minimize(loss)
init_op=tf.global_variables_initializer()
saver=tf.train.Saver()
start1=time.time()
with tf.Session() as sess:
    sess.run(init_op)
    R2=[]
    for i in range(1,2): #控制训练批次
        TRUE=[]
        PRED=[]
        for j in range (len(y_true)):#控制每批次训练的样本数
            sess.run(train_op,feed_dict={X:[x_true[j,:]],Y:[y_true[j,:]]})#[[]]是为了匹配占位的类型
            print('第%s批次第%s个样本训练的损失为:%s,真实值为：%s,预测值为:%s'% (i,j+1,sess.run(loss, feed_dict={X:[x_true[j,:]],Y:[y_true[j,:]]}),y_true[j,:],sess.run(y_pre,feed_dict={X:[x_true[j,:]],Y:[y_true[j,:]]})))
            TRUE.append(y_true[j,:].tolist())
            PRED.append(sess.run(y_pre,feed_dict={X:[x_true[j,:]],Y:[y_true[j,:]]}).tolist()[0])
end1=time.time()

 跑了一批

第1批次第1个样本训练的损失为:44.515533,真实值为：[8.34],预测值为:[[1.668004]]
第1批次第2个样本训练的损失为:22.748747,真实值为：[7.63],预测值为:[[2.8604357]]
第1批次第3个样本训练的损失为:19.92319,真实值为：[8.44],预测值为:[[3.9764595]]
第1批次第4个样本训练的损失为:2.6626563e-05,真实值为：[3.97],预测值为:[[3.9751601]]
第1批次第5个样本训练的损失为:38.861004,真实值为：[11.77],预测值为:[[5.536141]]
第1批次第6个样本训练的损失为:24.939627,真实值为：[11.8],预测值为:[[6.8060412]]
第1批次第7个样本训练的损失为:11.694864,真实值为：[11.2],预测值为:[[7.7802243]]
第1批次第8个样本训练的损失为:5.1589394,真实值为：[11.07],预测值为:[[8.79867]]
第1批次第9个样本训练的损失为:0.72628474,真实值为：[11.08],预测值为:[[10.227777]]
第1批次第10个样本训练的损失为:0.058379333,真实值为：[11.11],预测值为:[[11.351618]]
第1批次第11个样本训练的损失为:0.037325915,真实值为：[11.08],预测值为:[[10.886801]]
第1批次第12个样本训练的损失为:0.008513206,真实值为：[11.06],预测值为:[[11.152267]]
第1批次第13个样本训练的损失为:9.5740324e-05,真实值为：[11.01],预测值为:[[11.019785]]
第1批次第14个样本训练的损失为:1.72812e-05,真实值为：[10.99],预测值为:[[10.994157]]
第1批次第15个样本训练的损失为:0.033472456,真实值为：[10.88],预测值为:[[10.697045]]
第1批次第16个样本训练的损失为:0.00715772,真实值为：[10.87],预测值为:[[10.954603]]
第1批次第17个样本训练的损失为:0.00039784683,真实值为：[10.93],预测值为:[[10.910054]]
第1批次第18个样本训练的损失为:0.00052338885,真实值为：[10.96],预测值为:[[10.982878]]
第1批次第19个样本训练的损失为:0.0008995263,真实值为：[10.89],预测值为:[[10.860008]]
第1批次第20个样本训练的损失为:0.00014833717,真实值为：[10.82],预测值为:[[10.80782]]
中间省略...
第1批次第2663个样本训练的损失为:0.18928096,真实值为：[9.33],预测值为:[[8.894936]]
第1批次第2664个样本训练的损失为:0.09988854,真实值为：[9.29],预测值为:[[8.9739485]]
第1批次第2665个样本训练的损失为:1.451641,真实值为：[10.48],预测值为:[[9.275159]]
第1批次第2666个样本训练的损失为:1.4686363,真实值为：[10.79],预测值为:[[9.578127]]
第1批次第2667个样本训练的损失为:0.98703796,真实值为：[10.82],预测值为:[[9.826502]]
第1批次第2668个样本训练的损失为:1.0708082,真实值为：[11.12],预测值为:[[10.085201]]
第1批次第2669个样本训练的损失为:1.6277648,真实值为：[11.68],预测值为:[[10.404161]]
第1批次第2670个样本训练的损失为:1.009364,真实值为：[11.66],预测值为:[[10.655329]]

14.BPNN效果

TRUEs=[]
PREDs=[]

for i in TRUE:
    TRUEs.append(i[0])
for i in PRED:
    PREDs.append(i)  
TRUEmax,TRUEmin,PREDsmax,PREDsmin = train_test_split(TRUEs,PREDs,test_size=0.05,random_state=17)
plt.plot(TRUEmin)#测试数组
plt.plot(PREDsmin)#测试数组
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.title("DBSCAN-PBNN")  # 标题
plt.legend(['True','PBNN'])
plt.show()
# MSE
print(metrics.mean_squared_error(TRUEmin, PREDsmin)) # 8.107142857142858
# RMSE
print(np.sqrt(metrics.mean_squared_error(TRUEmin, PREDsmin))) # 2.847304489713536
# MAE
print(metrics.mean_absolute_error(TRUEmin, PREDsmin)) # 1.9285714285714286
# R2
print(metrics.r2_score(TRUEmin,PREDsmin))
#EVS
print(explained_variance_score(TRUEmin,PREDsmin))
#TIME
print(((end1-start1)/3600)*366)

0.11390565147753237
0.33749911329888316
0.2059761757637139
0.9660229469003566
0.9660237974708329
1.6406082673867544

非常优秀，但还是不够

15.做两次对比

plt.plot(TRUEmin,marker='o')#测试数组
plt.plot(PREDsmin,marker='>')#测试数组
plt.plot(DBSCANSVRGARESULT,marker='D')
plt.plot(DBSCANSVRRESULT,marker='s')
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.title("COMPARE(After noise reduction)")  # 标题
plt.legend(['True','DBSCAN-PBNN','DBSCAN-SVR-GA','DBSCAN-SVR'])
plt.show()

 

plt.plot(target_test,marker='o')#测试数组
plt.plot(SVRGARESULT,marker='P')
plt.plot(SVRRESULT,marker='D')
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.title("COMPARE(Before noise reduction)")  # 标题
plt.legend(['True','SVR-GA','SVR'])
plt.show()

 

不考虑原数据集的改动问题，单纯的从预测角度来看，t-SNE-DBSCAN-GASVR效果是很的不错，希望能对你们有所启发。