Leetcode--Java--42. 接雨水

Leetcode--Java--42. 接雨水 题目描述

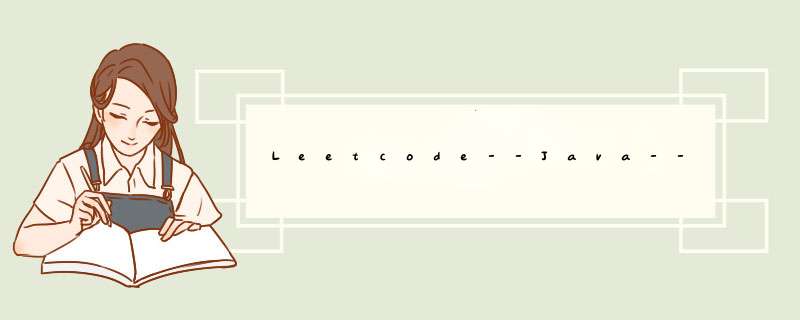
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

样例描述

思路

方法一：三次扫描法

存储左边、右边最大的高度，对于每一个位置，就是min（左边最大高度，右边最大高度）减去当前位置的高度，就是能存的水量遍历算左边最大高度是从左往右，算右边的要从右往左来依次更新，注意更新时是取上一个和当前位置height[i]比较，因为对于本身就是左边同时也是右边最大的，要存为本身位置。左端点和右端点不能存水，先直接存

方法二：单调栈（一次遍历）
参考题解思路如下：

代码

方法一：暴力法

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int left[] = new int[n];
        int right[] = new int[n];
        left[0] = height[0];
        right[n - 1] = height[n - 1];
        //左往右依次更新存储，每个点左边的最大值
        for (int i = 1; i < n; i ++ ) {
            //用上一个和当前自己的高度比较即可
            left[i] = Math.max(left[i - 1], height[i]);
        }
        //从右往左依次更新，每个点右边的最大值
        for (int i = n - 2; i >= 0; i --) {
            right[i] = Math.max(right[i + 1], height[i]);
        }
        int res = 0;
        //根据短板原理， 取左右里面的较小的，减去当前高度就是可存水量
        for (int i = 0; i < n; i ++ ) {
            res += Math.min(left[i], right[i]) - height[i];
        }
        return res;
    }
}

方法二：单调栈

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        if (n <= 2) return 0;
        int res = 0;
        //单调不增栈
        Deque stack = new linkedList<>();
        for (int right = 0; right < n; right ++ ) {
            //不断弹出低洼处，计算水量
            while (!stack.isEmpty() && height[right] > height[stack.peek()]) {
                int bottom = stack.pop();
                //如果栈空，说明没有左墙，也不能形成洼坑
                if (stack.isEmpty()) {
                    break;
                }
                int left = stack.peek();
                //底长度（要再减去1，举例子明显看出） 乘 高度(左右墙较小的减去坑洼高度)
                res += (right - left - 1) * (Math.min(height[left], height[right]) - height[bottom]);
            }
            //入栈放到后面，保证严格的不增栈
            stack.push(right);
        }
        return res;
    }
}