HashMap——如何保证容量为2的整数次幂？

HashMap——如何保证容量为2的整数次幂？

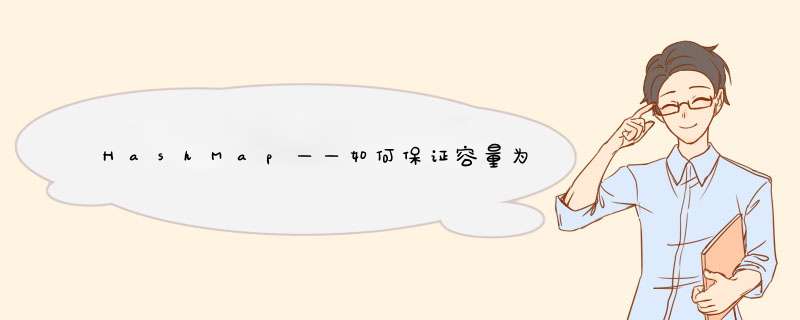
先来看一下HashMap内部元素存放的容器——成员变量table的定义

    
    transient Node[] table;

When allocated, length is always a power of two.
翻译过来：长度必须是2的整数次幂

HashMap的容量需要保证为2的整数次幂，但是HashMap提供了指定容量的构造方法，如：

    
    public HashMap(int initialCapacity, float loadFactor) {
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                    initialCapacity);
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                    loadFactor);
        this.loadFactor = loadFactor;
        this.threshold = tableSizeFor(initialCapacity);
    }

    
    public HashMap(int initialCapacity) {
        this(initialCapacity, DEFAULT_LOAD_FACTOR);
    }

如果使用者传入的不是2的整数次幂，比如10；HashMap如何保证容量为2的整数次幂呢？
先测试一下传入一个非2的整数次幂的容量初始化HashMap后的容量：

    @Test
    public void testCapacity() {
        HashMap map = new HashMap<>(5);
        // HashMap在添加第一个元素时初始化，所以需要put一个元素，不然反射获取到空数组，会报空指针异常
        map.put("","");
        System.out.println("通过反射获取到的HashMap容量为：" + getHashMapCapacity(map));
    }


    
    public static int getHashMapCapacity(HashMap map) {
        Class hashMapClass = HashMap.class;
        try {
            Field field = hashMapClass.getDeclaredField("table");
            field.setAccessible(true);
            Object[] objects = (Object[])field.get(map);
            return objects.length;
        } catch (NoSuchFieldException | IllegalAccessException e) {
            e.printStackTrace();
            return -1;
        }
    }

输出：

通过反射获取到的HashMap容量为：8

Process finished with exit code 0

传入5，初始化的容量是8；传入10，初始化的容量是16…
分析一下这个流程：
上面代码中使用的是这个构造：

    public HashMap(int initialCapacity) {
        this(initialCapacity, DEFAULT_LOAD_FACTOR);
    }

这个构造调用的另一个带加载因子的构造（阅读源码，会发现很多这样的写法）：

    public HashMap(int initialCapacity, float loadFactor) {
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                    initialCapacity);
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                    loadFactor);
        this.loadFactor = loadFactor;
        this.threshold = tableSizeFor(initialCapacity);
    }

这里对容量与加载因子的边界做了一系列判断（逻辑比较简单，并且不是本文重点），这个先不考虑；来看一下本文重点：

        this.threshold = tableSizeFor(initialCapacity);

这里调用了一个tableSizeFor方法，传入了初始化容量，所以我们来看一下这个方法：

    static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

这个方法的的作用就是返回>=参数的最小2的整数次幂，即转换为二进制后，有且只有一位为1；
输入cap，用n保存cap减一；经过下面一系列 *** 作，将n转换为大于n的最小2的n此幂-1的形式（即：前面全是0，后面全是1），再将n加一，就得到了2的整数次幂。这一些 *** 作就是：

        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;

考虑n的正常范围：
我们把n（32位）表示成0{32-x-1}1(0|1){x}（{x}表示前面的数字出现x次，这个表达式表示一个前面全是0的1后面有x个位，这个数共32位）：

*** 作 *** 作后n的值，后面x-m中m代表溢出的位数,先溢出不确定为1还是为0的，再溢出已经确定为1的；如果x-m为负，则代表已经溢出m-x个已经确定为1的位初始值0{32-x-1}1(0|1){x}n |= n >>> 10{32-x-1}11(0|1){x-1}n |= n >>> 20{32-x-1}1111(0|1){x-3}n |= n >>> 40{32-x-1}1111 1111(0|1){x-7}n |= n >>> 80{32-x-1}1111 1111 1111 1111(0|1){x-15}n |= n >>> 160{32-x-1}1111 1111 1111 1111 1111 1111 1111 1111(0|1){x-31}

总共右移了31位，去掉溢出的31位（所以后面不确定的数是x-31<0）：

除掉不确定的位数x => 还需要溢出31-x个已知为1的位；所以剩余为1的位数为：32-（31-x） = x+1位结论：n最终为：0{32-x-1}1{x+1}；即：
然后再将n+1，得到0{32-x-2}10{x+1}

举个例子，传入21，减一后为20（0000 0000 0000 0000 0000 0000 0001 0100）

*** 作 *** 作后n的值溢出位数初始值0000 0000 0000 0000 0000 0000 0001 01000n |= n >>> 10000 0000 0000 0000 0000 0000 0001 1111 -1n |= n >>> 20000 0000 0000 0000 0000 0000 0001 1111 —3n |= n >>> 40000 0000 0000 0000 0000 0000 0001 1111 ---- —7n |= n >>> 80000 0000 0000 0000 0000 0000 0001 1111 ---- ---- ---- —15n |= n >>> 160000 0000 0000 0000 0000 0000 0001 1111 ---- ---- ---- ---- ---- ---- ---- —31

表中标记的都是确定为1的数，"-"代表被溢出的数；
得到11111即31,31+1=32；返回32.

这里通过计算得到了>=初始化容量 的最小2的整数次幂；之后在put时调用resize()方法初始化容量。