一个质数有几个因数

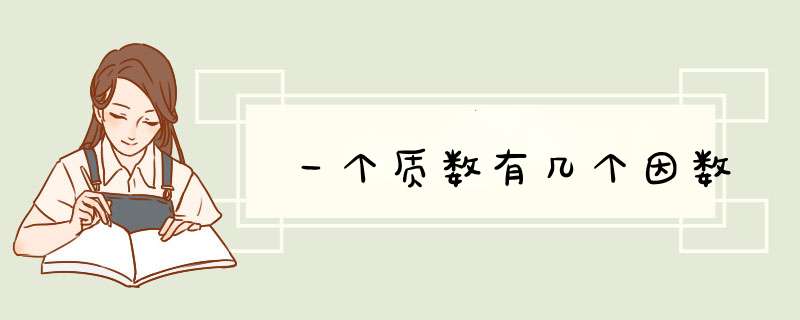
一个质数有2个因数。

质数的定义为在大于1的自然数中，除了1和它本身以外不再有其他因数，故质数只有1和它本身2个因数，若a是b的因数且a是质数，则称a是b的质因数。

公因数只有1的两个非零自然数叫做互质数，1个非零自然数的正因数的个数是有限的，其中最小的是1，最大的是它本身，而一个非零自然数的倍数的个数是无限的。

质数具有许多独特的性质：

1、质数p的约数只有两个：1和p。

2、初等数学基本定理：任一大于1的自然数，要么本身是质数，要么可以分解为几个质数之积，且这种分解是唯一的。

3、质数的个数是无限的。

4、若n为大于或等于2的正整数，在n到n!之间至少有一个质数。

5、所有大于10的质数中，个位数只有1、3、7、9。

合数是什么：

合数是指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。与之相对的是质数，而1既不属于质数也不属于合数。最小的合数是4。其中，完全数与相亲数是以它为基础的。

一个质数最多只有两个因数并且只有两个因数。因为质数本身的定义就是。只有一和它本身两个因数的数叫做质数。因此质数只能有且只有两个因数。所以质数最多有两个因数。合数是除了一和它本身以外还有其他的因素所以合数最少有三个因数。这是质数和因数的区别。

2个。

质数的定义为在大于1的自然数中，除了1和它本身以外不再有其他因数。故质数只有1和它本身2个因数。

拓展资料：

假如a*b=c（a、b、c都是整数)，那么我们称a和b就是c的因数。需要注意的是，唯有被除数，除数，商皆为整数，余数为零时，此关系才成立。 反过来说，我们称c为a、b的倍数。在研究因数和倍数时，不考虑0。

若a是b的因数，且a是质数，则称a是b的质因数。例如2，3，5均为30的质因数。6不是质数，所以不算。7不是30的因数，所以也不是质因数。

公因数只有1的两个非零自然数,叫做互质数。

1个非零自然数的正因数的个数是有限的，其中最小的是1，最大的是它本身。而一个非零自然数的倍数的个数是无限的。

---