1到20的平方表

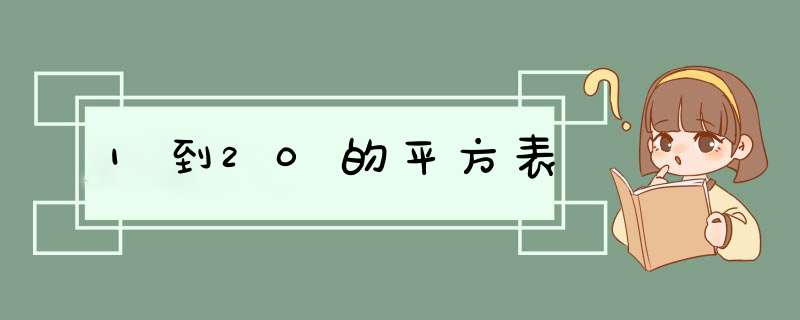
1到20的平方表如图所示：

平方计算方法

a的平方表示a×a，简写成a²，也可写成a×a(a的一次方乘a的一次方等于a的2次方）。

例如：4×4=16，8×8=64，平方符号为²。

除了代数中的计算，平方也是面积的单位，例如平方米、平方厘米等。

扩展资料

图形面积的计算方法

1、长方形面积=长×宽

2、平行四边形面积=底×高

3、三角形面积=底×高÷2

4、圆的面积=半径×半径×圆周率

5、梯形的面积=（上底+下底）×高÷2

换算关系

平方千米（平方公里）km²，1平方千米（平方公里）=1,000,000平方米

平方分米，dm²，1平方分米=0.01平方米

平方厘米，cm²，1平方厘米=0.000 1平方米

平方毫米，mm²，1平方毫米=0.000 001平方米

小学1到20的平方数的口诀如下

1²=1   2²=4    3²=9

4²=16    5²=25   6²=36

7²=49   8²=64    9²=81

10²=100    11²=121    12²=144

13²=169    14²=196    15²=225

16²=256    17²=289   18²=324

19²=361    20²=400

扩展资料

其他平方数列举以下

21² = 441 ，22² = 484， 23² = 529 ，24² = 576， 25² = 625 ，26² = 676， 27² = 729 ，28² = 784 ，29² = 841， 30² = 900，

31² = 961， 32² = 1024， 33² = 1089 ，34² = 1156 ，35² = 1225， 36² = 1296 ，37² = 1369 ，38² = 1444， 39² = 1521 ，40² = 1600，

41² = 1681， 42² = 1764 ，43² = 1849， 44² = 1936， 45² = 2025 ，46² = 2116 ，47² = 2209 ，48² = 2304 ，49² = 2401， 50² = 2500。

平方数（或称完全平方数），是指可以写成某个整数的平方的数，即其平方根为整数的数。

平方数也称正方形数，若n为平方数，将n个点排成矩形，可以排成一个正方形。若将平方数概念扩展到有理数，则两个平方数的比仍然是平方数，例如，  。若一个整数没有除了 1 之外的平方数为其因子，则称其为无平方数因数的数。

著名数学家毕达哥拉斯发现有趣奇数现象：将连续奇数相加，每次的得数正好就产生完全平方数。 如：1 + 3(=2²) + 5(=3²) + 7(=4²) + 9(=5²) + 11(=6²) + 13(=7²)……

在奇数和平方数之间有着密切的重要联系。一个整数是完全平方数当且仅当相同数目的点能够在平面上排成一个正方形的点阵，使得每行每列的点都一样多。

参考资料：百度百科-平方数

。

---