tan37度°等于多少

tan37度约等于0.75355405。

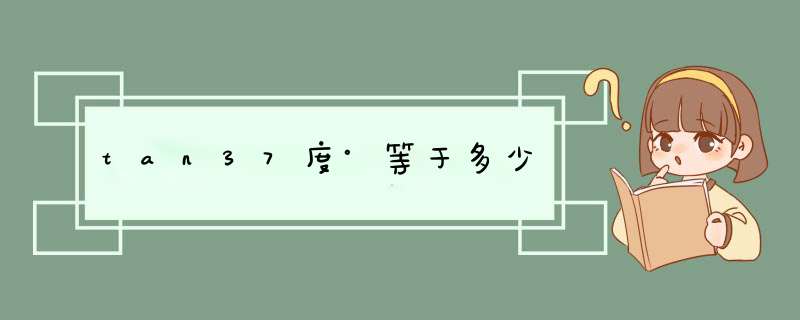
在直角三角形ABC中，∠C=90度，AB是∠C的对边c，BC是∠A的对边a，AC是∠B的对边b，正切函数就是tanA=a/b，即tanA=BC/AC。正切的常用值一般为tan30°，tan45°，tan60°等等。

因此，将tan37°化为小数大约等于0.75355405，用分数表示大约等于3/4。

tan37°=0.75355405。

在Rt△ABC（直角三角形）中，∠C=90°，AB是∠C的对边c，BC是∠A的对边a，AC是∠B的对边b，正切函数就是tanB=b/a，即tanB=AC/BC。

扩展资料：

在平面三角形中，正切定理说明任意两条边的和除以第一条边减第二条边的差所得的商等于这两条边的对角的和的一半的正切除以第一条边对角减第二条边对角的差的一半的正切所得的商。

法兰西斯·韦达(Fran&ccedilois Viète)曾在他对三角法研究的第一本著作《应用于三角形的数学法则》中提出正切定理。现代的中学课本已经甚少提及，例如由于中华人民共和国曾经对前苏联和其教育学的批判，在1966年至1977年间曾经将正切定理删除出中学数学教材。不过在没有计算机的辅助求解三角形时，这定理可比余弦定理更容易利用对数来运算投影等问题。

---