bezier曲线的应用

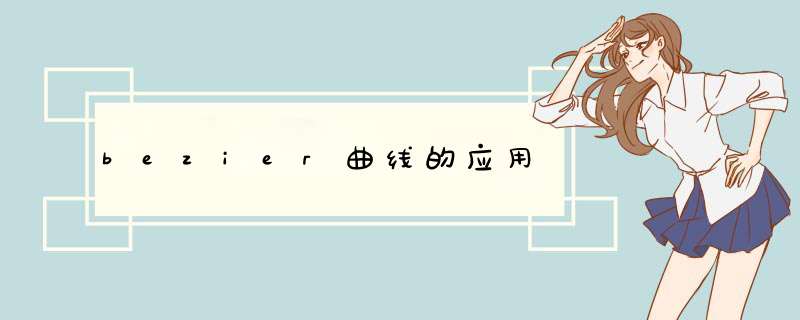
Bezier曲线会落在 convex hull 之内，不会有不可预期形状

Bezier曲线有整体修正(globally modification)之特性 – 也就是更动任一控制点会更改整条曲线之形状

Bezier曲线所有混成函数的和为 1

Bezier曲线的反曲点之数少於控制多边形之边数

Bezier曲线与一平面的相交点之数 少於 该平面与控制多边形之的相交点之数

<2>一、Bezier曲线定义：

给定n+1个控制顶点Pi(i=0~n) ，则Bezier曲线定义为：

P(t)=∑Bi,n(t)Pi t∈[0,1]

其中：Bi,n(t)称为基函数。

Bi,n(t)=Ci nti (1-t)n-i

Ci n=n!/(i!(n-i)!)

二、Bezier曲线性质

1、端点性质：

a）P(0)=P0, P(1)=Pn, 即：曲线过二端点。

b）P’(0)=n(P1-P0), P’(1)=n(Pn-Pn-1)

即：在二端点与控制多边形相切。

2、凸包性：Bezier曲线完成落在控制多边形的凸包内。

3、对称性：由Pi与Pn-i组成的曲线，位置一致，方向相反。

4、包络性：Pn (t)=(1-t)Pn-1 (t)+tPn-1 (t)

在CAD/CAM中，常采用Bezier曲线曲面，这样便于理解曲线/曲面。但采用Bezier形式的曲线曲面不能精确的表示二次曲线和二次曲面，如球体和圆。将多项式改为有理形式，不仅能精确表示二次曲线和二次曲面，且增加了设计的自由度。重复的进行两点线性插值，可以构造Bezier Curve。重复的进行两点有理插值，可以构造有理Bezier Curve。

与控制顶点类似，有理Bezter曲线上的点可映射为Bezter曲线上的点或对应的控制多边形上的点。在透视投影使用理形式与非有理形式产生相同投影时，有理Besier曲线曲面和有理B样条曲线曲面继承了Bezier曲线曲面和B样条曲线曲面的简单、优美的特性。这种形式，数学上的分析及几何特性的掌握了解都比其他4D空间(wx、wy、wz、w)方法和单纯的3D空间有理形式要简单和容易。

现在，有理曲线曲面不仅仅用于表示和构造二次曲线曲面。对有理曲线曲面的权因子该如何选取往往不很清楚，而且有理形式的计算比非有理形式复杂，但是，由于其构造特性，现在人们已经开始考虑有理Bezter和有理B样条曲线曲面的应用

你这里的16个点是属于控制点还是曲面上的点

如果是曲面上的点, 16个显得少了这样需要NURBS曲面反算, 这个可不简单, 需要查相关论文

如果是控制点, 直接加入opengl的命令array里就行

至于控制点的生成, 简单说来就是通过少数已知点, 加上一定的参数控制, 来生成剩余的点

->需要反算或者视做点云进行拟合(也是需要特殊算法的)

正算是有NURBS的控制点算出曲面上的点, 这个有公式, 所以相对简单

反算的话我只知道不简单, 呵呵具体不会

打开blender“创建”--“贝塞尔曲线”创建一根曲线。

通过“物体”--“转换为”--“曲线/融球/曲面/文字转网格”，把曲线转换为“模型网格”。

右边的“修改器”中选择添加“表皮”。

点击“应用”后曲线就变成可以编辑的“立体模型”了。

还有一种更好用的方法，可以创建曲线后，再创建一“圆形曲线”作为线的形状。

选择“曲线”，然后点选右边的“数据”，

倒角物体，选择我们创建的圆形曲线“贝塞尔曲线”，然后我们曲线就变“圆形的线条”了。

最后别忘记“alt+c”键，选择“曲线/融球/曲面/文字转网格”，转换为网格模型。

以上就是关于bezier曲线的应用全部的内容，包括:bezier曲线的应用、问个opengl里通过所有已知点（未知控制点），生成曲面的方法、blender怎么曲线变成面blender曲线如何转换成模型等相关内容解答，如果想了解更多相关内容，可以关注我们，你们的支持是我们更新的动力！