如何excel计算积分

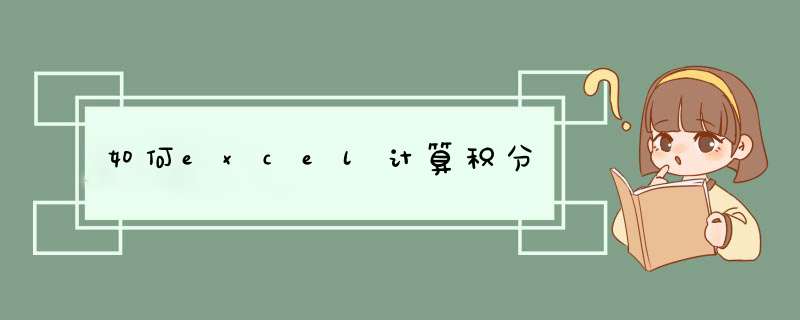
Excel中只能实现带积分符号的函数显示，而不能实现积分的运算。

显示函数可以使用插入公式来进行编辑显示。

专业的公式编辑器可以编辑所有的公式功能。它无论是Word、Excel还是PowerPoint中都可以使用。

退出公式编辑器就可以见到完整的公式了。

同时需要注意的是，公式编辑器是OFFICE在安装时的一个选项，如果在安装时此项没有选的话，是不能进行公式编辑的。遇到没有安装的情况，可以通过重新更改安装OFFICE来解决。

积分是微分的逆运算，即知道了函数的导函数，反求原函数。在应用上，积分作用不仅如此，它被大量应用于求和，通俗的说是求曲边三角形的面积，这巧妙的求解方法是积分特殊的性质决定的。

感觉不需要使用m文件，根据你给的代码，函数f(x)的参数x没有作用啊。具体需求是什么？

下面是求积分

f=@(x) exp(05x)sin(x+pi/6);

s=quad(f,0,pi);

定积分计算详细步骤：

1、分析积分区间是否关于原点对称，即为[-a,a]，如果是，则考虑被积函数的整体或者经过加减拆项后的部分是否具有奇偶性，如果有，则考虑使用“偶倍奇零”性质简化定积分计算。

2、考虑被积函数是否具有周期性，如果是周期函数，考虑积分区间的长度是否为周期的整数倍，如果是，则利用周期函数的定积分在任一周期长度的区间上的定积分相等的结论简化积分计算。

3、考察被积函数是否可以转换为“反对幂指三”五类基本函数中两个类型函数的乘积，或者是否包含有正整数n参数，或者包含有抽象函数的导数乘项，如果是，可考虑使用定积分的分部积分法计算定积分。

4、考察被积函数是否包含有特定结构的函数，比如根号下有平方和、或者平方差（或者可以转换为两项的平和或差的结构），是否有一次根式，对于有理式是否分母次数比分子次数高2次以上；是否包含有指数函数或对数函数。

5、对于具有这样结构的积分，考虑使用三角代换、根式代换、倒代换或指数、对数代换等；换元的函数一般选取严格单调函数；与不定积分不同的是，在变量换元后，定积分的上下限必须转换为新的积分变量的范围。

依据为：上限对上限、下限对下限；并且换元后直接计算出关于新变量的定积分即为最终结果，不再需要逆变换换元！

题主给出的积分函数，用matlab 求解，可以这样做

1、确定x在-300，300中，取若干个x(i)数据，如

x=-300:10:300;

2、使用for循环语句，将x(i)代入积分函数I(x)中，使用int函数计算其积分值，同时将值赋值给Ix数组变量中

for n=1:600/t+1

syms x

A_1=int(cos((pi(x^2))/2),x,a1(1,n),a2(1,n));

A_2=int(sin((pi(x^2))/2),x,a1(1,n),a2(1,n));

Ix(n)=1000(lambda/(2L))((A_1)^2+(A_2)^2);

end

3、最后用plot函数，绘出其x—I(x)的图形

运行程序，可以得到如下结果。

误差界eps%被积函数为f(x)=(x^3+sin(x))/x;积分区间为[03,08]

#include<stdioh>

#include<stdlibh>

#include<mathh>

int main(void)

{

/ int i,j,n;

float d=(float )malloc(sizeof(float)N);

float x=(float )malloc(sizeof(float)N);

float y=(float )malloc(sizeof(float)N);

float u=(float )malloc(sizeof(float)N);

free(a);free(b);free(c);free(d);free(x);free(y);free(l);

return 0;

/

double b=08;

double a=03;

double h=00; //

double eps=10e-5;//误差界eps

int kmax=20; //最大递推次数

double T1=00,S1=00,C1=00,R1=00,T2=00,S2=00,C2=00,R2=00;

double sum;

double x,fx;

int i;

h=b-a;

T1=h/2((pow(a,3)+sin(a))/a+(pow(b,3)+sin(b))/b);

printf("T1:%1312f\n",T1);

for(int k=0;k<kmax;k++)

{

h=(b-a)/(pow(2,k+1));

x=(double )malloc(sizeof(double)int(pow(2,k)));

for(i=0;i<pow(2,k);i++)

{

x[i]=a+(2i+1)h;

}

fx=(double )malloc(sizeof(double)int(pow(2,k)));

sum=00;

for(i=0;i<pow(2,k);i++)

{

fx[i]=(pow(x[i],3)+sin(x[i]))/x[i];

sum+=fx[i];

}

T2=T1/2+sumh;

printf("T2:%1312f\n",T2);

S2=T2+(T2-T1)/3;

printf("S%d:%1312f\n",int(pow(2,k)),S2);

if(k<2)

{

if(k==1)

{

C2=S2+(S2-S1)/15;

printf("C1:%1312f\n",C2);

}

}

else

{

C2=S2+(S2-S1)/15;

printf("C%d:%1312f\n",int(pow(2,k-1)),C2);

R2=C2+(C2-C1)/63;

printf("R%d:%1312f\n",int(pow(2,k-2)),R2);

if(fabs(R2-R1)<eps)

break;

R1=R2;

}

T1=T2;S1=S2;C1=C2;

free(x);free(fx);

}

printf("所求积分I=%1312f\n",R2);

return 0;

}

24个基本积分公式：

1、∫kdx=kx+C(k是常数)。

2、∫x^udx=(x^u+1)/(u+1)+c。

3、∫1/xdx=ln|x|+c。

4、∫dx=arctanx+C21+x1。

5、∫dx=arcsinx+C21x。

（配图1）

24个基本积分公式还有如下：

6、∫cosxdx=sinx+C。

7、∫sinxdx=cosx+C。

8、∫sec∫csc2xdx=tanx+Cxdx=cotx+C2。

9、∫secxtanxdx=secx+C。

10、∫cscxcotxdx=cscx+C。

11、∫axdx=+Clna。

12、[∫f(x)dx]'=f(x)。

13、∫f'(x)dx=f(x)+c。

14、∫d(f(x))=f(x)+c。

15、∫1/(a^2-x^2)dx=(1/2a)ln|(a+x)/(a-x)|+c。

16、∫secxdx=ln|secx+tanx|+c。

17、∫1/(a^2+x^2)dx=1/aarctan(x/a)+c。

18、∫1/√(a^2-x^2)dx=arcsin(x/a)+c。

19、∫sec^2xdx=tanx+c。

20、∫shxdx=chx+c。

21、∫chxdx=shx+c。

22、∫thxdx=ln(chx)+c。

23、令u=1x2，即∫u=23u+C3312122=3u+C=3(1x)+C12d(1x)2。

24、令u=cosx=2，即∫u=22+C=u+C=cosx+C。

不定积分：

不定积分的积分公式主要有如下几类：含ax+b的积分、含√（a+bx）的积分、含有x^2±α^2的积分、含有ax^2+b（a>0）的积分、含有√（a²+x^2） （a>0）的积分、含有√（a^2-x^2） （a>0）的积分、含有√（|a|x^2+bx+c） （a≠0）的积分、含有三角函数的积分、含有反三角函数的积分、含有指数函数的积分、含有对数函数的积分、含有双曲函数的积分。

画图程序：

x=linspace(-02,07,100);

f1=x;

f2=31055x^5-515x^4+22945x^3-04345x^2+11845x;

plot(x,f1,x,f2,'r');

首先是求交点，也就是求方程的根，如下：

f=@(x)31055x^5-515x^4+22945x^3-04345x^2+01845x;

z=fzero(f,07)

z =

06704

两个根为06704和0；

然后就是分别求积分，也就是与X轴的面积，再相减就是所围的面积

>> data=@(x)31055x^5-515x^4+22945x^3-04345x^2+11845x;

y1=quad(data,0,06704)

y1 =

02459

>> f=@(x)x;

y2=quad(f,0,06704)

y2 =

02247

>> ff=y1-y2

ff =

00212

ff即为面积！！！

定积分

import static javalangMath;

public class homeworkfour {

// 0~1区间n等分

private static int n = 100000;

// 随便定义个曲线e的x次方, 取其x在0~1的定积分;

public static double f(double x) {

double f;

f = pow(E, x);

return f;

}

// 梯形法求定积分

/

x0: 坐标下限, xn: 坐标上限

/

public static double getDefiniteIntegralByTrapezium(double x0, double xn) {

double h = abs(xn - x0) / n;

double sum = 0;

for (double xi = 0; xi <= xn; xi = xi + h) {

sum += (f(xi) + f(xi + h)) h / 2;

}

return sum;

}

/

x0: 坐标下限, xn: 坐标上限

/

// 矩形法求定积分, 右边界

public static double getDefiniteIntegralByRectangle1(double x0, double xn) {

//h: 步长

double h = abs(xn - x0) / n;

double sum = 0;

for (double xi = 0; xi <= xn; xi = xi + h) {

sum += f(xi + h) h;

}

return sum;

}

// 矩形法求定积分, 左边界

public static double getDefiniteIntegralByRectangle2(double x0, double xn) {

double h = abs(xn - x0) / n;

double sum = 0;

for (double xi = 0; xi <= xn; xi = xi + h) {

sum += f(xi) h;

}

return sum;

}

/

测试定积分

/

public static void main(String[] args) {

Systemoutprintln(getDefiniteIntegralByTrapezium(0, 1));

Systemoutprintln(getDefiniteIntegralByRectangle1(0, 1));

Systemoutprintln(getDefiniteIntegralByRectangle2(0, 1));

}

}

以上就是关于如何excel计算积分全部的内容，包括:如何excel计算积分、如何在matlab的m文件里编写个积分程序、定积分计算详细步骤是什么等相关内容解答，如果想了解更多相关内容，可以关注我们，你们的支持是我们更新的动力！