使平面适合3D中的一组点：scipy.optimize.minimize与scipy.linalg.lstsq

使平面适合3D中的一组点：scipy.optimize.minimize与scipy.linalg.lstsq

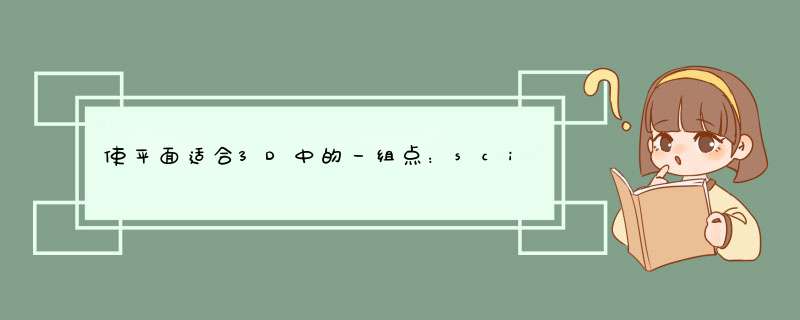
最小二乘（

scipy.linalg.lstsq

）保证收敛。实际上，有一个封闭形式的解析解（由给出

(A^T A)^-1A^Tb

（其中

^T

矩阵转置和

^-1

矩阵求逆）

但是，标准优化问题通常无法解决-我们不能保证找到一个最小值。然而，对于给定的公式，发现一些

a, b, c

这样

z = a*x + b*y +c

，我们有一个线性优化问题（的约束条件和目标是变量，我们正在努力，以优化线性）。线性优化问题通常可以解决，因此

scipy.optimize.minimize

应收敛到最优值。

注意：即使我们这样做，它在约束中也是线性的

z = a*x + b*y + d*x^2 + e*y^2 +f

-我们不必将自身限制为的线性空间

(x,y)

，因为我们已经有了这些点

(x, y, x^2,y^2)

。对于我们的算法，这些看起来就像矩阵中的点

A

。因此，实际上我们可以使用最小二乘法获得一个高阶多项式！

简要说明一下： 实际上，所有不使用精确解析解的求解器通常都停在实际答案的可接受范围内，因此，很少有我们获得 精确
解的情况，但往往如此最后，我们接受它在实践中是准确的。此外，即使是最小二乘解算器也很少使用分析解决方案，而是求助于更快的方法，例如牛顿法。

如果要更改优化问题，那将不是事实。我们通常可以为某些类型的问题找到一个最佳值（其中最大的一类称为凸优化问题-
尽管有很多非凸问题可以在某些条件下找到一个最佳值）。

如果您想了解更多信息，请查看Boyd和Vandenberghe的Convex
Optimization。第一章不需要太多的数学背景，它概述了一般的优化问题及其与线性和凸规划等可解决的优化问题的关系。