三力平衡汇交定理

三力平衡汇交定理 三力平衡汇交定理的证明

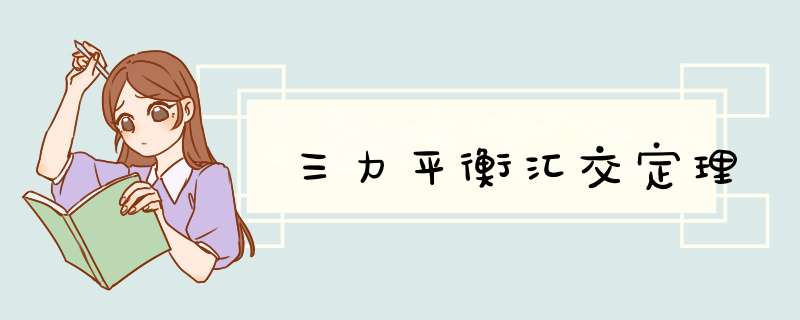
如图1所示，在F1、F2、F3三力的作用线上分别取不共线的三点A、B、C 并相互连接，组成平面ABC。

现考虑三力对AB轴的矩，由于F1、F2通过AB 轴，故对AB轴的力矩均为零。

由三力平衡知,三力对任一轴的力矩之和均为零。

由此知，F3对AB轴的力矩也为零，故F3与AB轴的位置关系只可能有平行或相交两种情形（具体请参见力矩平衡）。

由这两种情形的任一种均可得出F3必在平面ABC上的结论。

同理可证，F1、F2也必在平面ABC上。

于是必有F1、F2、F3三力共面。

如图2所示，在刚体的A、B、C三点上分 别作用三个力F1、F2、F3，使刚体处于平衡。

其中F1、F2的作用线汇交于一点 O。

根据力的可传性，将力F1和F2移到汇交点O，然后根据力的平行四边形法则，求得其合力F12，则F3应与 F12平衡。

根据二力平衡公理，力F3与F12共线。

所以，力F3必定与力F1和F2共面，且通过力F1和F2的汇交点O。

（1）假设作用在刚体上的不平行的三个力分别为F1、F2、F3。

建立以F1作用点为原点，作用线为X轴，方 向为X轴正方向的空间直角坐标系。

根据力的可传性，将F2、F3的作用点沿其力的作用线平移至XOY平面 内，设其坐标分别为：A2(x2，y2，0)；A3(x3，y3，0)（2）根据力矩平衡和受力平衡列出方程： ，, 对于Y、Z方向，列相同的力和力矩平衡方程。

（3）解方程组，得：Fz2=Fz3=0，F2、F3和F1在XOY平面上，再由二力平衡的条件得出共点。

（同直接证明）Fz2·Fz3≠0，设F2、F3尾线连线交平面XOY于A4（x4，y4，0），解得：故，焦点位于X轴上，所以F2、F3和F1在XOZ平面上，再由二力平衡的条件得出共点。