最小正周期是多少

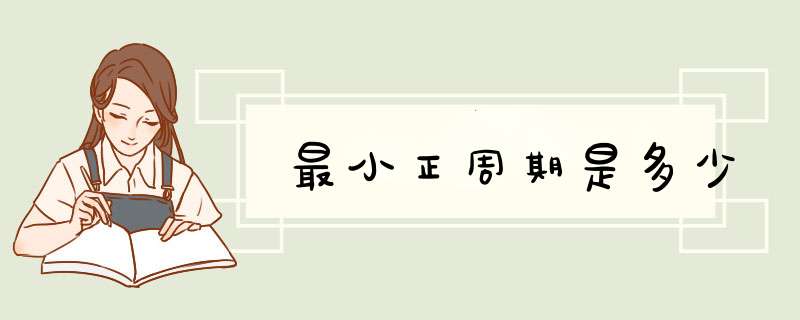
y=cosx的最小正周期是2π ，y=Asin(ωx+ψ)或y=Acos(ωx+ψ)的最小正周期用公式计算：T=2π/ω。y=Atan(ωx+ψ)或y=cot(ωx+ψ)的最小正周期用公式计算：T=π/ω。

对于正弦函数y=sinx, 自变量x只要并且至少增加到x+2π时，函数值才能重复取得正弦函数和余弦函数的最小正周期是2π。y=Asin(ωx+φ), T=2π/ω（其中ω必须u003e0）。

扩展资料：

这类题目是通过三角函数的恒等变形，转化为一个角的一种函数的形式，用公式去求，其中正余弦函数求最小正周期的公式为T=2π/|ω| ，正余切函数T=π/|ω|。

函数f(x)=Asin(ωx+φ)和f(x)=Acos(ωx+φ)(A≠0,ωu003e0）的最小正周期都是；函数f(x)=Atan(ωx+φ)和f(x)=Acot(ωx+φ)(A≠0,ωu003e0）的最小正周期都是。

运用这一结论，可以直接求得形如y=Af(ωx+φ)(A≠0,ωu003e0）一类三角函数的最小正周期（这里“f”表示正弦、余弦、正切或余切函数）。